Плотность тока термоавтоэмиссии (продолжение)

В § 5 мы детально исследовали распределение электронов эмиссии по энергиям. Эти результаты позволят нам вычислить величину плотности тока термоавтоэмиссии, поскольку функция распределения электронов эмиссии является подынтегральным выражением в соответствующей формуле для плотности тока. Вычисления удобно проводить в NED-представлении. Как и в § 5, рассмотрим два случая.

1. ЕТ эмиссия

Подставляя (5.5) в (4.3), получаем

. (6.1)

Замена переменной

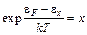(6.2)

и условие позволяет переписать выражение (6.1) в виде

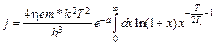. (6.3)

Интеграл в (6.3) равен

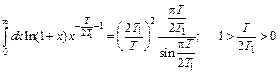. (6.4)

Подставляя (6.4) в (6.1) и делая несложные преобразования, окончательно для j получаем

. (6.5)

Величина

(6.6)

носит название плотность тока автоэмиссии или плотность тока Фаулера-Нордгейма, по имени исследователей, впервые рассмотревших задачу об автоэлектронной эмиссии. Формула (6.5) с учетом влияния конечной температуры впервые была получена Мерфи и Гудом.

Перепишем формулу (6.6), подставляя в нее выражения для а и Т ₁ согласно (5.2) и (5.3)

. (6.7)

В этом выражении обращает на себя внимание очень резкая, экспоненциальная, зависимость плотности тока автоэмиссии от напряженности электрического поля Е и работы выхода j. Это обстоятельство, как мы увидим ниже, играет определяющую роль в целом ряде физических явлений, в которых имеет место автоэлектронная эмиссия.

В эмиссионной электронике используется смешанная система единиц, в которой плотность тока исчисляется в А/см², работа выхода в эВ, напряженность электрического поля в В/см. Если принять, что эффективная масса электрона m равна массе свободного электрона, то можно записать расчетные формулы для термоавтоэмиссии

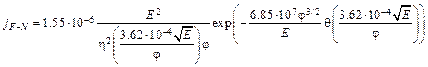(6.8)

и

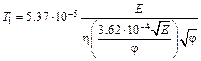. (6.9)

В формуле (6.9) температура инверсии Т ₁ получается в градусах Кельвина.

2. ТЕ эмиссия

Подставляя (5.15) в формулу (4.3), получаем

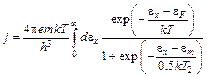. (6.10)

Делая замену переменных:

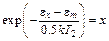(6.11)

и учитывая, что 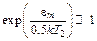, переписываем (6.10) в виде

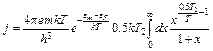. (6.12)

Интеграл равен

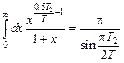; . (6.13)

Подставляя (6.13) в (6.12), учитывая определения работы выхода (2.8) и эффекта Шоттки (2.11), окончательно получаем

. (6.14)

Величина

(6.15)

носит название плотности тока термоэмиссии с поправкой Шоттки или плотности тока Ричардсона-Шоттки. В отсутствие электрического поля формула (6.15) описывает термоэмиссию или испарение электронов. Формула (6.14) с дополнительным множителем, учитывающим влияние электрического поля, была получена впервые Мерфи и Гудом.

Если принять эффективную массу равной массе свободного электрона, то расчетные формулы, описывающие ТЕ эмиссию, выглядят следующим образом

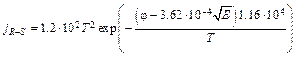, (6.16)

. (6.17)

Дата добавления: 2014-01-06