Плотность потока энергии через эмиссионную поверхность

Как будет показано во второй главе, важную роль в энергетическом балансе термоавтокатода играет поверхностный источник тепла, непосредственно связанный с эмиссией. Из изложенного в пятом параграфе следует, что функция распределения эмиттированных электронов отличается от энергетического распределения электронов проводимости катода. Это приводит к тому, что средняя энергия, уносимая электроном эмиссии, отлична от той средней энергии, которую приносит электрон проводимости из глубины катода к границе эмиссии, что и обуславливает поверхностный источник тепла (в алгебраическом смысле, т.е. разогрев или охлаждение). Плотность потока энергии j_T через эмиссионную поверхность, аналогично (4.1), определяется выражением

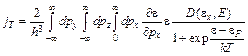. (7.1)

Вычисления j_T удобно проводить в TED-представлении. Делая замену переменных в (7.1) согласно процедуре (4.5), получаем

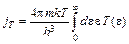. (7.2)

1. ЕТ эмиссия

Используя (5.24), записываем

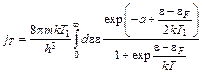, (7.3)

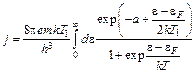. (7.4)

Сравнение (7.3) и (7.4) позволяет при вычислении (7.3) обойтись без квадратур, используя результаты § 6:

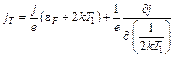. (7.5)

Подставляя в (7.5) (6.5), окончательно получаем

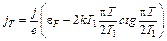. (7.6)

Формула (7.6) интересна в том отношении, что второе слагаемое в скобках меняет свой знак при Т = Т ₁. Как будет показано во второй главе, это соответствует смене процесса разогрева катода на процесс охлаждения. Отсюда и получила величина Т ₁ название температуры инверсии. Впервые на это обстоятельство указал Ноттингам.

2. ТЕ эмиссия

Подставляя (5.34) в (7.2) и (4.6), получаем

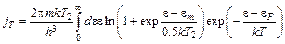, (7.7)

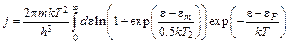. (7.8)

Сравнивая (7.7) и (7.8), можно записать

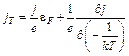. (7.9)

Используя (6.14), из (7.9) получаем

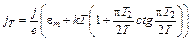. (7.10)

На рис. 7.1 показаны области значений электрических полей и температур, при которых можно использовать полученные выше формулы.

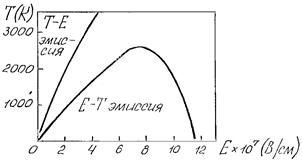
Рис. 7.1

Дата добавления: 2014-01-06