Определение Н.В. отрезка прямой и углов его наклона к плоскости или проекции методом прямоугольного треугольника

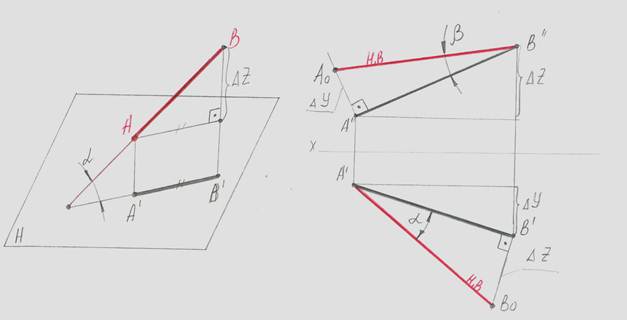
Угол наклона прямой с плоскостью – есть угол между прямой и ее проекцией на данную плоскость.

Для определения Н.В. отрезка нужно построить прямоугольный треугольник, у которого один конец есть проекция на плоскость, а другой - разность расстояний концов отрезка до этой плоскости.

Проекция плоских углов.

Теорема: Если обе стороны любого угла параллельны плоскости проекции,

его на эту плоскость он проецируется в Н.В.(без искажения)

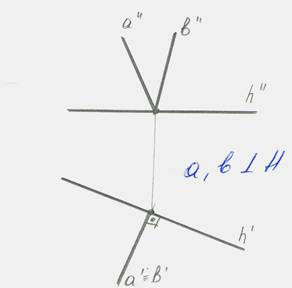
если одна сторона прямого угла параллельна плоскости проекций. А другая сторона ей не перпендикулярна, то прямой угол проецируется на эту плоскость без искажений.

Если горизонталь и любая другая прямая перпендикулярны, то на чертеже их горизонтальные проекции перпендикулярны Пример 1: Из точки А. опустить перпендикуляр на прямую υ	Если фронталь и любая другая прямая перпендикулярны, то на чертеже их фронтальные проекции перпендикулярны. Пример 2: Построить горизонтальную проекцию прямой a┴h
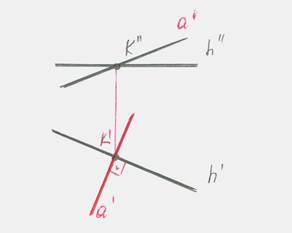
Пример 3: Определить расстояние от точки А до прямой h

Плоскость. Задание плоскость на чертеже. Принадлежность точки и прямой плоскости.

I Положение плоскости в пространстве определяется:

a) Тремя точками не лежащими на одной прямой.

b) Прямой и точкой, вне этой прямой

c) Двумя пересекающимися прямыми

d) Двумя параллельными прямыми

e) Следами плоскости.

αh- горизонтальный след плоскости

αv- фронтальный след плоскости

αx- точка схода следов

След плоскости- это прямая, по которой плоскость пересекается с плоскостью проекций.

II Классификация плоскостей.

а) плоскости уровня – это плоскости, параллельные плоскостям проекции

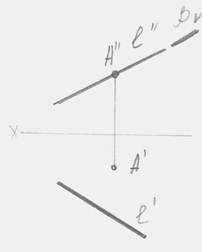
б) Проецирующие плоскости- называется плоскости перпендикулярные к одной из плоскостей проекции.

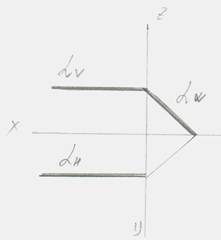
α(A,B,C)┴H горизонтальная проекция	β(l,A)┴V фронтальная проекция	α┴W профильная проекция

в) Общего положения – плоскости не перпендикулярные ни к одной из плоскостей проекции

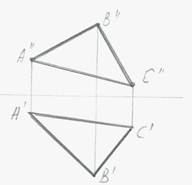
III Прямая и точка в плоскости. Принадлежность их плоскости.

· Прямая принадлежит плоскости если она проходит через две точки, лежащие а плоскости.

· Если она проходит через точку принадлежащую плоскости и параллельную прямой, находящейся в той же плоскости.

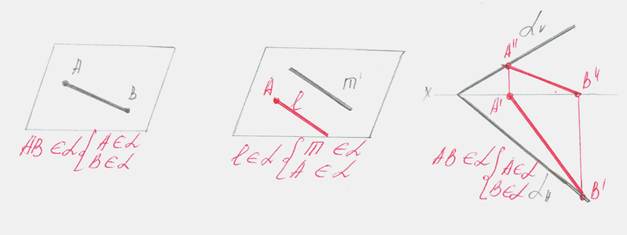
· Точка принадлежит плоскости, если она лежит на прямой лежащей в данной плоскости

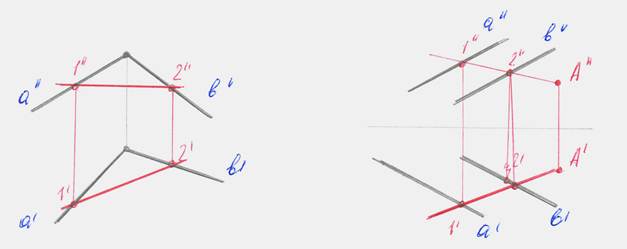
Из прямых принадлежащих плоскости, выделяют прямые особого положения(частичного положения). Это горизонтали и фронтали, линии наибольшего наклона.

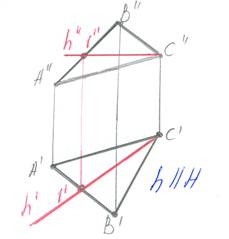
	Горизонталь к плоскости- это прямая параллельная горизонтальной плоскости проекции. h- горизонталь
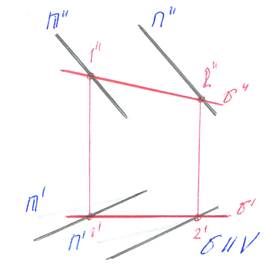
	Фронталь плоскости – это прямая параллельная фронтали плоскости проекции υ- фронталь

Дата добавления: 2014-01-06