
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямая угловая засечка
|
|
|
|
Обратная геодезическая задача на плоскости
Прямая геодезическая задача на плоскости
В геодезии есть две стандартные задачи: прямая геодезичеcкая задача на плоскости и обратная геодезическая задача на плоскости.
Прямая геодезическая задача - это вычисление координат X2, Y2 второго пункта, если известны координаты X1, Y1 первого пункта, дирекционный угол α и длина S линии, соединяющей эти пункты. Прямая геодезическая задача является частью полярной засечки, и формулы для ее решения берутся из набора формул (2.7):
 (2.8)
(2.8)
Обратная геодезическая задача - это вычисление дирекционного угла α и длины S линии, соединяющей два пункта с известными координатами X1, Y1 и X2, Y2 (рис.2.5).
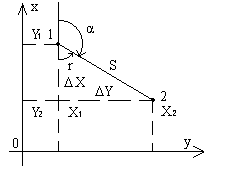
Рис.2.5
Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна S, катеты равны приращениям координат точек 1 и 2 (ΔX = X2 - X1, ΔY = Y2 - Y1), а один из острых углов равен румбу r линии 1-2.
Если Δ X 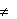 00 и Δ Y
00 и Δ Y 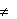 00, то решаем треугольник по известным формулам:
00, то решаем треугольник по известным формулам:
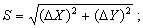 (2.9)
(2.9)
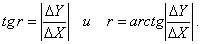 (2.10)
(2.10)
Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому на основании (1.22) находим:
 (2.11)
(2.11)
Общий порядок нахождения дирекционного угла линии 1-2 включает две операции:
- определение номера четверти по знакам приращений координат Δ>X и ΔY (рис.1.4-а),
- вычисление α по формулам связи (1.22) в соответствии с номером четверти.
Контролем правильности вычислений является выполнение равенства:
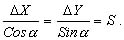 (2.12)
(2.12)
Если ΔX = 0.0, то
S = ¬ΔY¬;
и α = 90o 00' 00" при ΔY > 0,
α = 270o 00' 00" при ΔY < 0.
Если ΔY = 0.0, то
S = ¬ΔX¬
и α = 0o 00' 00" при ΔX > 0,
α = 180o 00' 00" при ΔX < 0.
Для решения обратной задачи в автоматическом режиме (в программах для ЭВМ) используется другой алгоритм, не содержащий тангенса угла и исключающий возможное деление на ноль:
 (2.13)
(2.13)
если ΔY => 0o, то α = a,
если ΔY < 0o, то α = 360o - a.
Сначала рассмотрим так называемый общий случай прямой угловой засечки, когда углы β1 и β2 измеряются на двух пунктах с известными координатами, каждый от своего направления с известным дирекционным углом (рис.2.6).
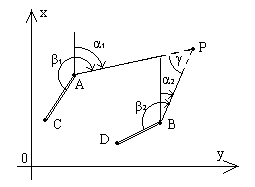
Рис.2.6
Исходные данные: XA, YA, αAC,
XB, YB, αBD
Измеряемые элементы: β 1, β2
Неизвестные элементы: X, Y
Если αAC и αBD не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D.
Графическое решение. От направления AC отложить с помощью транспортира угол β1 и провести прямую линию AP; от направления BD отложить угол β2 и провести прямую линию BP; точка пересечения этих прямых является искомой точкой P.
Аналитическое решение. Приведем алгоритм варианта, соответствующий общему случаю засечки:
- вычислить дирекционные углы линий AP и BP
 (2.14),
(2.14),
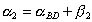 (2.15)
(2.15)
- написать два уравнения прямых линий
для линии AP Y - YA= tgα1 * (X - XA),
для линии BP Y - YB= tgα2 * (X - XB) (2.16)
- решить систему двух уравнений и вычислить неизвестные координаты X и Y:
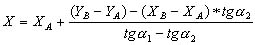 (2.17),
(2.17),
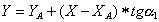 (2.18)
(2.18)
Частным случаем прямой угловой засечки считают тот случай, когда углы β1 и β2 измерены от направлений AB и BA, причем угол β1 - правый, а угол β2 - левый (в общем случае засечки оба угла - левые) - рис.2.7.
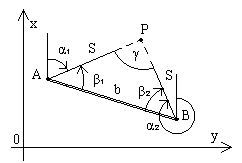
Рис.2.7
Решение прямой угловой засечки методом треугольника соответствует частному случаю засечки. Порядок решения при этом будет такой:
- решить обратную задачу между пунктами A и B и получить дирекционный угол αAB и длину b линии AB,
- вычислить угол γ при вершине P, называемый углом засечки,
 (2.19)
(2.19)
- используя теорему синусов для треугольника APB:
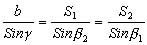 (2.20)
(2.20)
вычислить длины сторон AP (S1) и BP (S2),
- вычислить дирекционные углы α1 и α2:
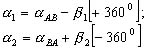 (2.21)
(2.21)
- решить прямую задачу от пункта A к точке P и для контроля - от пункта B к точке P.
Для вычисления координат X и Y в частном случае прямой угловой засечки можно использовать формулы Юнга:
 (2.22)
(2.22)
От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геодезическую задачу между пунктами A и B и получить дирекционный угол αAB линии AB и затем вычислить углы в треугольнике APB при вершинах A и B
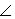 BAP = αAB - (αAC + β1) и
BAP = αAB - (αAC + β1) и 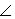 ABP = (αBD + β2) - αBA.
ABP = (αBD + β2) - αBA.
Для машинного счета все рассмотренные способы решения прямой угловой засечки по разным причинам неудобны. Один из возможных алгоритмов решения общего случая засечки на ЭВМ предусматривает следующие действия:
- вычисление дирекционных углов α1 и α2,
- введение местной системы координат X'O'Y' с началом в пункте A и с осью O'X', направленной вдоль линии AP, и пересчет координат пунктов A и B и дирекционных углов α1 и α2 из системы XOY в систему X'O'Y' (рис.2.8):
X'A = 0, Y'A = 0,
 (2.23),
(2.23),
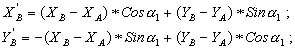 (2.24),
(2.24),
- запись уравнений линий AP и BP в системе X'O'Y':
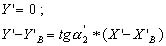 (2.26)
(2.26)

Рис.2.8
и совместное решение этих уравнений:
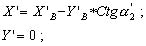 (2.27)
(2.27)
- перевод координат X' и Y' из системы X'O'Y' в систему XOY:
 (2.28)
(2.28)
Так как Ctgα2' = - Ctgγ и угол засечки γ всегда больше 0о, то решение (2.27) всегда существует.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 2113; Нарушение авторских прав?; Мы поможем в написании вашей работы!