Системы счисления, используемые в ЭВМ

Для изображения чисел используются определенные приемы и правила, которые носят название систем счисления. Все известные системы счисления делятся на две группы: по­зиционные и непозиционные системы счисления.

Непозиционной системой счисления называется такая система, в которой значение символа (цифры, знака, иероглифа) не зависит от позиции этого символа в изображаемом числе.

В позиционных системах счисления, наоборот, значение сим­вола (цифры, знака, иероглифа) зависит от позиции этого символа в изображаемом числе.

Непозиционные системы, как более простые, появились истори­чески гораздо раньше позиционных систем. Ими пользовались древ­ние славяне, китайцы и другие народы. До наших дней дошла одна из разновидностей непозиционных систем - так называемая римская система счисления.

В этой системе символ I всегда изображает число 1, символ V - пять, Х - десять, L - пятьдесят, С - сто, D - пятьсот, М - тысячу и т.д.

Строго говоря, римская система - смешанная система, в ней присутствуют и элементы позиционности. При изображении чисел в этой системе используется правило; если символ с меньшим "весом" стоит справа от символа с большим "весом", то изображаемое ими число есть суммаих "весов" (так, например, число VI есть 5+1=6); если символ с меньшим "весом" стоит cлева. от символа с большим "весом", то изображаемое ими число есть разница их "ве­сов" (число IV есть 5-1=4).

Пример. Десятичное число 1986 в римской системе будет иметь вид M.CM.LXXX.VI. Приведем еще ряд примеров записи чисел в римской системе счисления: MCCCLXXX (1380), MMI I (2002), MCMXCIX (1999).

Непозиционные системы счисления обладают двумя существенны­ми недостатками. Во-первых, при увеличении диапазона представимых чисел увеличивается и число различных символов в изобража­емых числах. Во-вторых, очень сложны правила выполнения даже са­мых простых арифметических действий.

Позиционные системы счисления обладают тем чрезвычайно важ­ным свойством, что все числа, и большие, и малые, могут быть за­писаны с помощью конечного набора различных символов.

Кроме того, правила арифметических действий с многоразряд­ными числами могут быть резюмированы в виде таблиц сложения и ум­ножения и выучены раз и навсегда наизусть (так собственно и по­ступают в первом и втором классах нашей школы).

Изобретение позиционных систем имело неоценимые последствия для дальнейшего развития человеческой цивилизации. Впервые такие системы счисления стали использовать древние шумерийцы, вавило­няне и индусы.

В позиционных системах счисления любое число Х изображается в виде полинома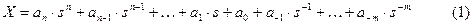

В этом выражении a_n, a_n-1, …, a_-m называются коэффи­циентами, а s - основанием системы счисления.

Значение любого коэффициента в изображаемом числе может ле­жать в диапазоне от 0 до s-1. В настоящее время во всех странах мира используется десятичная система счисления, представляющая собой позиционную систему счисления с основанием s = 10. Коэф­фициенты a_n, a_n-1, …, a_-m при изображении чисел в деся­тичной системе счисления могут принимать значения в диапазоне 0 …9.

Для краткости вместо записи числа в виде полинома (1) запи­сывают только последовательность коэффициентов этого полинома и запятую (или точку), отделяющую целую и дробную части числа. Когда мы пишем Х = 87,56, то подразумеваем величину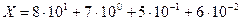

Значение первой цифры числа слева от запятой полностью соот­ветствует значению изображенной цифры (говорят, что ее "вес" ра­вен единице); значение следующей по порядку слева цифры равно десятикратному значению изображаемой цифры ("вес" этой цифры уже равен 10) и т.д.

Значение цифры справа от запятой равняется десятой ее части (ее "вес" равен 0,1), следующей - сотой части цифры (ее "вес" - 0,01) и т.д.

В принципе, роль основания способно играть любое целое чис­ло, большее единицы.

Возьмем, например, десятичное число 327. Вполне логично это число записать и как 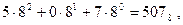где индекс 8 у числа 507 указывает, что мы имеем дело с числом, при записи которого вместо привычного нам основания s = 10 ис­пользовано основание s=8. Числа, записанные в системе счисления с основанием s= 8, называются восьмеричными числами.

То же самое десятичное число 327 можно записать и в виде .

Числа, записанные в системе счисления с основанием 16, на­зываются шестнадцатеричными числами. Часто, чтобы указать, что представлена шестнадцатеричная запись некоторого числа, в конце этой записи помещается строчная латинская буква h. Например, последнюю запись 147₁₆ можно представить как 147h.

Простейшей позиционной системой счисления является система счисления с основанием s=2.

В этой системе число 327 запишется как

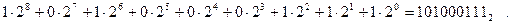
Преимущество использования в качестве основания s числа 2 состоит в том, что требуется только две различные цифры (0 и 1) для записи любого числа. Некоторым недостатком двоичной системы является то, что для изображения числа в двоичной форме требуется примерно в 3,3 раза больше цифр по сравнению с десятичной формой записи.

Подобно тому, как для записи десятичных чисел используют десять различных цифр (О…9), для записи двоичных чисел применяют две цифры (0 и 1), восьмеричных - восемь (О…7) и шестнадцатеричных - 16. Так как только десять цифр из шестнадцати можно обозна­чить общепринятыми арабскими цифрами 0…9, то для записи остальных шести цифр используют первые шесть символов латинского алфавита - А, В, С, D, Е и F (символ А обозначает цифру "десять", сим­вол В - "одиннадцать", С - "двенадцать", D - "тринадцать",, Е -"четырнадцать" и F - "пятнадцать").

Так, например, шестнадцатеричное число Х₁₆=2Е соответст­вует десятичному числу Х₁₀ = 46, так как 2 х 16 + 14 = 46.

С дробными числами при любом основании обращаются так же, как и в десятичной системе. Необходимо лишь учитывать то обстоя­тельство, что конечная дробь в одной системе счисления может стать периодической в другой. Так, например, 0,38₁₆ =0,21875₁₀, но 0,2₁₀ = 0,333...₁₆.

В ЭВМ используются позиционные системы счисления с основа­ниями2, 8, 10 и 16. Основной системой счисления для ЭВМ является двоичная система. Во-первых, в этой системе счисления, как уже говорилось, для изображения любых чисел необходимы комбинации только двух различных цифр 0 и I. Эти две цифры можно изобразить элементами, имеющими два различных состояния. Одному состоянию, причем любому, можно поставить в соответствие цифру "0", а другому - "I". Такие эле­менты называются двухпозиционными (две позиции - два состояния) и они исключительно легко реализуются технически.

Для сравнения укажем, что для изображения одного десятично­го разряда числа необходимо иметь элемент, имеющий десять четко выраженных различных состояний. В принципе, такие элементы можно разработать, но они будут значительно сложнее и дороже двухпози­ционных элементов. Во-вторых, логика выполнения арифметических операций в двоичной системе счисления наиболее проста. Это нагляд­но видно на примере сравнения таблиц умножения одноразрядных де­сятичных чисел с одной единственной таблицей умножения двоичных чисел, имеющей вид

0 х 0 =0 0 х 1 =0 1 х 0 =0 1 х 1 =1

Из приведенных примеров видно, что десятичная система счис­ления крайне неудобна для использования в ЭВМ, но она общепринята, с ней человечество связано своими языками, она наиболее понятна для анализа.

Поэтому, несмотря на свои недостатки, она используется в ЭВМ. Чаще всего в десятичной системе ЭВМ воспринимает исходные данные и в десятичной системе она должна выдавать результаты вы­числений.

Для того чтобы ввести в ЭВМ десятичные числа, отобразить их состояниями двухпозиционных элементов, используется так назы­ваемая двоично-десятичная форма представления десятичных чисел. В этой форме каждая десятичная цифра многоразрядного числа изоб­ражается в виде четырехразрядного двоичного числа (двоичной те­трады).

Например, десятичное число Х₁₀ = 183,65 в двоично-десятич­ной форме будетиметь вид: Х_2-10 = 0001 1000 0011, 0110 0101.

Нельзя путать двоично-десятичную форму записи числа и дво­ичной записью того же числа. В первом случае основание системы счисления остается равным десяти - только коэффициенты при этом основании выражены в двоичной форме.

Восьмеричная и шестнадцатеричная формы записи чисел, в основном, используются при программировании задач для ЭВМ и для ведения компактных записей чисел во время отладки программ. Достоинством этих форм записи числа является их компактность, с одной стороны, и легкость, перевода из двоичной записи в восьмеричную (шестнадцатеричную) и наоборот, с другой стороны.

Например, чтобы перевести шестнадцатеричное число Х₁₆ = 1FА,0FВ в двоичную форму, необходимо просто представить каждую шестнадцатеричную цифру двоичным четырехразрядным эквивалентом. В итоге получим:

0001 1111 1010,0000 1111 1011

Ниже приведены различные формы записи первых 16-ти чисел натурального ряда.

Десятичное число Двоичное число Шестнадцатеричное число Двоично-десятичное число

Дата добавления: 2014-01-06