Формы представления числовой информации в ЭВМ

16 10000 10 0001 0110

F 0001 0101

E 0001 0100

D 0001 0011

С 0001 0010

B 0001 0001

А 0001 0000

9 1001 9 1001

8 1000 8 1000

7 111 7 0111

6 110 6 0110

5 101 5 0101

4 100 4 0100

3 11 3 0011

2 10 2 0010

1 1 1 0001

0 0 0 0000

Необходимо особо подчеркнуть, что правила выполнения ариф­метических операций над многоразрядными числами, представленными в позиционных системах счисления с различными основаниями, одни и те же. Отличие составляют лишь таблицы сложения и умножения одноразрядных чисел.

Рассмотрим пример. Пусть нам необходимо найти произведение двух восьмеричныхчисел Х₈ = 35 (это число соответствует десятич­ному числу 29) и У₈ = 12 (это число соответствует десятичному числу 10).

Будем умножать эти числа обычным "столбиком". При умножении будем использовать заранее составленные таблицы умножения и сложения одноразрядных восьмеричных чисел.

I

I

и

I

I

I

б

Ответ: Х₈ х Y₈ = 35 х 12 = 442₈

х ^{35 х} 12 * 72 ⁺^-

Умножая 2 на 5 в восьмеричной системе, получаем результат 12₈ (см. таблицу 2). Это соответствует 10 в десятичной системе счисления. Следовательно, согласно общеизвестным правилам, в дан­ном разряде записывается число 2, а единица переноса запоминает­ся. Умножая далее 2 на 3, получаем, также как и в десятичной сис­теме счисления, результат "б", а с учетом запомненной единицы пе­реноса записываем цифру 7. Таким образом, результатом умножения восьмеричного числа 35 на цифру 2 будет восьмеричное число 72. Аналогично умножается множимое 35 на следующую цифру множи­теля (35₈ х 1=35).

При сложении 72₈ и 350₈ необходимо пользоваться таблицей сло­жения (табл.3). Так, например, при сложении 7 + 5 получаем число 14. Поэтому в соответствующем разряде записывается цифра 4 и за­поминается единица переноса в старший соседний разряд. Оконча­тельный ответ в восьмеричной системе счисления 442₈ соответству­ет десятичному числу 360 (36 х 10).

Мы своими языками сроднились с десятичной системой, и нам не составляет никакого труда произнести вслух любое десятичное чис­ло (все наши числительные ориентированы на эту систему). Иное дело числа, записанные в других системах счисления! Попробуйте прочесть вслух восьмеричное число 442₈. Это не четыреста сорок два!

Небезынтересно отметить, что исключительная роль десятка при формировании общепринятой системы счисления, несомненно, свя­зано с тем обстоятельством, что при расчетах древние люди поль­зовались пальцами рук. А их, как известно, десять.

В то же время из истории становления математики известны случаи использования древними народами позиционных систем счис­ления с другими основаниями. Так, например, в древнем Вавилоне использовалась система счисления с основанием 60. Как отголосок этой системы деление одного часа на 60 минут, а одной минуты на 60 секунд. То же ка­сается и деления угловых градусов на угловые минуты, а угловых минут на угловые секунды.

В английском и немецком языках, в отличие от русского язы­ка, числительные "одиннадцать" и "двенадцать" лингвистически не связаны с числом "десять". Это наталкивает на мысль, что и чис­ла "II" и "12" были когда-то у этих народов основаниями систем счисления.

И лишь позже многочисленные позиционные системы счисления были вытеснены более удобной длятех времен десятичной системой счисления.

Обычный порядок вычислений на ЭВМ таков. Исходные числовые данные вводятся в ЭВМ в обычной для человека десятичной форме (например, с помощью клавиатуры устройства ввода). ЭВМ имеют в своем составе специальные устройства, называ­емые шифраторами, которые осуществляют автоматический перевод вводимой десятичной информации в двоично-десятичную форму. Затем, по специальному алгоритму, числа из двоично-десятичной формы пе­реводятся в двоичную систему счисления (в некоторых ЭВМ в систе­му команд включены специальные команды, осуществляющие перевод чиселиз двоично-десятичной системы счисления в двоичную и на­оборот).

Все необходимые вычисления, связанные с решением конкретной задачи, производятся в двоичной системе счисления. Если необхо­димо выдать какие-то результаты вычислений в десятичной системе, то эти данные переводятся сначала в двоично-десятичную форму, а уже затем с помощью устройств, называемых дешифраторами, числа преобразуются в заданную десятичную форму (например, печатаются на бланке принтером или высвечиваются на экране дисплея).

Такой порядок вычислений используется при решении научно-технических задач. В таких задачах количество исходных числовых данных и результатов вычислений сравнительно невелико по сравне­нию с количеством операций, необходимых для решения задачи.

В то же время имеется большой класс задач, отличающийся обилием входной и выходной информации и требующих для своего ре­шения небольшого числа вычислительных операций (например, начис­ление зарплаты рабочим и служащим, расчет коммунальных услуг и т.д.). Для таких задач описанный выше порядок вычислений не яв­ляется оптимальным из-за низкой производительности процессора ЭВМ - слишком много времени процессор будет тратить на многочис­ленные переводы числовой информации из двоично-десятичной формы в двоичную и наоборот. Для решения указанных задач разработаны специальные методы вычислений непосредственно в двоично-десятич­ной форме.

В современных ЭВМ общего назначения обязательно присутству­ют как группа команд, выполняющих операции в двоичной системе счисления (команды двоичной арифметики - основные команды для любого типа ЭВМ), так и группа команд, выполняющих операции в двоично-десятичной форме (команды десятичной арифметики).

При программировании для представления исходных данных десятичные числа записываются как обычно, а вот при записи чисел в других системах в конце числа ставится спецификатор – буква, которая указывает, в какой системе записано это число: в конце двоичного числа ставится буква b (binary), в конце восьмеричного числа – буква O (octal) или буква q (буква «O» очень похожа на ноль, поэтому для меньшей путаницы рекомендуется использовать букву «q»), а в конце шестнадцатеричного числа – буква h (hexadecimal). Ради общности спецификатор, а именно букву d (decimal), разрешается указывать и в конце десятичного числа, но обычно этого не делают.

Примеры:

Десятичные числа: 25, -386, +4, 25d, -386d Двоичные числа: 101b, -11000b

Восьмеричные числа: 74q, -74q Шестнадцатеричные числа: 1Afh, -1AFh

В ЭВМ используются две формы представления числовой инфор­мации; естественная форма (с фиксированной запятой) и полулога­рифмическая форма (с плавающей запятой).

Естественная форма характеризуется тем, что местоположение запятой, отделяющей целую часть числа от его дробной части стро­го фиксировано. Это означает, что если n-разрядное число в каком-то блоке ЭВМ (в памяти или в процессоре) представлено комбина­циями n-двухпозиционных элементов, то запятая всегда строго фиксирована после К-ого элемента, т.е. всегда заранее известно, сколько двухпозиционных элементов выделено для изображения целой части числа, и сколько двухпозиционных элементов для изображения его дробной части.

К-ым элементом может быть, в принципе, любой по порядку эле­мент. На практике, с целью максимального упрощения правил выпол­нения арифметических операций, используются две основные разно­видности естественной формы представления числовой информации.

В первом случае запятая фиксируется перед самым левым циф­ровым разрядом числа. В этом случае все числа, представимые в ма­шине, должны быть меньше единицы.

В другом случае запятая фиксируется после самого правого цифрового разряда числа. В этом случае все числа, представимые в ЭВМ, должны быть только целыми, т.е. без дробной части. При использовании полулогарифмической формы любое число Х представляется в виде: где S - основание системы счисления; P - порядок числа (целое число со знаком); M - мантисса числа X. Мантисса числа должна лежать в пределах 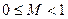. В ЭВМ вводится мантисса числа, знак мантиссы, порядок числа и знак порядка.

Полулогарифмическая форма наиболее удобна при проведении на ЭВМ научно-технических расчетов, в то время как естественная форма предпочтительна при решении задач логического характера. Поскольку задачи логического характера составляют 80-90% от об­щего числа решаемых на ЭВМ задач, то естественная форма является основной формой представления числовой информации. В ЭВМ общего назначения использовались обе формы представле­ния числовой информации.

Машинные коды. Кодом называется любое обозначение, отличное от общеприня­того. Общепринято, например, положительные числа отмечать знаком "+" (или, вообще, не указывать их знак), а отрицательные числа отмечать знаком «-». Числа разного знака необходимо уметь изоб­ражать состояниями двухпозиционных элементов при вводе их в ма­шину.

Для изображения знака числа вводится дополнительный разряд, называемый знаковым, причем состояние "0" этого разряда изобра­жает знак "+", а состояние "I" - знак "-". Такое изображение чи­сел со знаком называется прямым кодом. Число Х в прямом коде бу­дем условно изображать как IXIпр. В числах, представленных в естественной форме, знаковый разряд помещается непосредственно перед числом. Таким образом, прямой код числа, представленного в естественной форме (это в полной мере отно­сится и к мантиссе числа, представленного в полулогарифмической форме), образуется по следующему правилу. Если число Х положи­тельно, т.е. Х = +0,Х1Х2,…Хn (Х1Х2,…Хn - цифровые разряды числа), то IXIпр = 0,Х1Х2…Хn; если число Х отрицательно, т.е. Х = -0,Х1Х2…Хn, то [Х]пр = 1,Х1Х2…Хn.

Примеры: Х = +0.1011 [Х]пр = 0,1011 У= -0,1101 [У]пр = 1.1101

Как известно, правила сложения многоразрядных чисел отли­чаются от правил вычитания. Чтобы по существующим правилам вы­полнять эти операции, ЭВМ должна иметь в своем составе два само­стоятельных устройства - сумматор и вычитатель.

Но оказалось, что можно обойтись только одним устройством - сумматором, если изображать числа, участвующие в операции, в специальных кодах (в дополнительном коде или в обратном коде). Положительные числа в этих кодах полностью совпадают с прямым кодом числа.

Обратный код отрицательного числа (будем изображать его как [Х]о) образуется так. В знаковом разряде числа записывается " I ", а в цифровых разрядах, по отношению к исходному числу про­изводитсязамена цифры "0" на "I", а "I" на "0". Пример: Х=-0,1101 [X]о =1,0010.

Дополнительный код отрицательного числа, получается из обрат­ного кода прибавлением "I" к младшему цифровому разряду: [X]д = [X]о +2^-n, где п - число, соответствующее коли­честву цифровых разрядов.

Пример: Х= -0,1101 [X]д=1,0010 +2^-4 = 1,0011.

Иногда в машинных кодах для изображения знака используется не один знаковый разряд, а два. Такие коды называются модифици­рованными. Знак "+" в этих кодах представляется комбинацией "00", а "-'' - комбинацией "11".

Раньше уже указывалось, что при выполнении операций над чис­лами, представленными в естественной форме, ни в коем случае нельзя допускать, чтобы какой-либо промежуточный результат пре­высил определенные допустимые пределы. Допустимые пределы - это так называемая разрядная сетка, т.е. двухпозиционные элементы, выделенные для хранения цифровых разрядов результатов.

Разрядная сетка ЭВМ однозначно указывает, сколько двухпозиционных элементов выделено для изображения цифровых раз­рядов числа и сколько для изображения знака числа. Выход за допустимые пределы результата называется также переполнением разрядной сетки.

При переполнении разрядной сетки происходит полнейшее искажение результата - и по величине, и по знаку. Поясним это на примерах.

1. Пусть даны два числа Х = +0,1101 и У = +0,1001. При сложении этих чисел получим: 0,1101 ⁺ 0,1001= 1,0110

Несмотря на положительные знаки слагаемых в знаковом разряде результата появилась "1", т.е. сумма как бы получилась отрицательной. Получилось это потому, что при сложении чисел получился перенос из старшего цифрового разряда в знаковый.

2. Даны два отрицательных числа Х = -0,1101 и У = -0,1001

[X]д = 1,0011 [Y]д= 1,0111

1,0011 + 1,0111 = 10,1010

Для самой левой единицы в разрядной сетке места нет. Поэтомурезультатом будет величина 0,1010, не соответствующая искомо­мурезультату,ни по величине, ни по знаку.

Естественно, случаи переполнения разрядной сетки необходи­мооперативно обнаруживать с выдачей соответствующего сообщений.

Переполнение разрядкой сетки легко обнаруживается при сло­жении чисел в модифицированных кодах. Рассмотрим предыдущие при­меры.

00,1101 + 00,1001 =01,0110

11,0011 + 11,0111 = 110,1010

Как только в результате выполнения операции сложения чисел в естественной форме с применением модифицированного кода в зна­ковых разрядах оказываются комбинации "01" или "10", то это озна­чает, что произошло переполнение разрядной сетки.

Для чисел, представленных в полулогарифмической форме, пере­полнение разрядной сетки при сложении мантисс не страшно. В этом случае разрядная сетка включает два знаковых разряда мантиссы, цифровые разряды мантиссы, знак порядка и цифровые разряды вели­чины порядка.

Если переполнение разрядной сетки имеет место, то ЭВМ ав­томатически производит сдвиг содержимого мантиссы (вместесо зна­ковыми разрядами) вправо на один разряд с одновременным увеличе­нием величины порядка на единицу.

Диапазон представимых чисел в ЭВМ. Разрядная сетка ЭВМ и форма представления числовой информа­ции однозначно определяют диапазон представимых чисел в ЭВМ и. точность получаемых результатов.

Если числовая информация представлена в естественной форме, то диапазон представимых чисел лежит в пределах: или 1>Х³О (для случая, когда запятая фиксирована левее самого старшего ци­фрового разряда) или 1£Х<2ⁿ -1 (для случая, когда запятая фиксирована правее самого младшего цифрового разряда).

Если числовая информация представлена в полулогарифмичес­кой форме, то диапазон представимых чисел будет лежать в преде­лах

0.0…01£ |X|£0.11…1*2^11…1

Процессоры современных персональных компьютеров поддерживают следующие форматы числовых величин: целые числа в естественной форме – байт, слово (2 байта) и двойное слово (4 байта), числа в полулогарифмической форме – 4 байта и 8 байт.

Значение	Описание	Дробная часть	Размер
Байт	Числа от 0 до 255 целого типа	Отсутствует	1 байт
Целые	Числа от-32768 до 32767 целого типа	Отсутствует	2 байта
Длинное целое	Числа от- 2147483648 до 2147483647 целого типа	Отсутствует	4 байта
С плавающей точкой	Числа от-3.402823*10^38 до 3.4023823*10^38		4 байта
С плавающей точкой (8 байт)	Числа от -1.79769313486232*10^308до 1.79769313486232*10^308		8 байт

2.3.Кодирование алфавитно-цифровой информации.

Современные ЭВМ обрабатывают не только числовую, но и ал­фавитно-цифровую информацию, содержащую цифры, буквы, знаки пре­пинания, математические и другие символы. Именно такой характер имеет экономическая, планово-производственная, учетная, бухгалтерская и другая информация, содержащая наименование предметов, фамилии людей и т.д. Возможность ввода, обработки и вывода алфавитно-цифровой информации важна и для решения чисто математических задач, так как это позволяет оформлять результаты вычислений в удобной форме сприменением таблиц, графиков, комментариев и рисунков.

Алфавитно-цифровые символы позволяют оформлять алгоритмы решения задач в наиболее удобной для человека форме (для этого разработаны специальные алгоритмические языки) и вводить в ЭВМ, поручая ЭВМ по специальным программам перевод вводимых алгорит­мов с алгоритмического языка на внутренний машинный язык машины, т.е. в программу, записанную в системе команд ЭВМ. Программы, осуществляющие такой перевод, называются трансляторами, компиля­торами и интерпретаторами.

Совокупность всех символов, используемых в ЭВМ, представля­ет собойее алфавит. Каждый вводимый в ЭВМ символ с помощью устройства ввода пре­образуется в соответствующий двоичный код фиксированной длины. В настоящее время чаще всего для кодирования символов используется 8-разрядный двоичный код, т.е. байт. Посредством байта можно ко­дировать до 256 различных символов. (Это вытекает из формулы Хартли – N=2ⁿ. 256=2⁸)В настоящее время используется несколько различных кодировок: Windows 1251, Кодовая страница 766 MS-DOS, KOI-8R, ISO 8859-5.

Особенности кодировки букв русского алфавита. Итак, для кодирования символа используется один байт. Естественно, одного байта недостаточно для кодировки символов всех известных языков. Поэтому поступили так. Первые 128 значений байта (числа 0 – 7F) были выделены для кодирования символов латинского алфавита (строчных и прописных), арабских цифр 0 – 9 и некоторых других стандартных символов.

Для кодирования символов других национальных алфавитов отводятся числа с 80 по ff (или с128 по 255 в десятичной системе счисления).

К сожалению, имеет место несколько различных кодировок именно букв русского алфавита. Так, например, в кодировке Win 1251 русской прописной букве А соответствует число CO (192), а строчной букве я – число FF (255). А в кодировке KOI-8 числом CO (192) кодируется не прописная буква А, а строчная буква ю. В скобках указаны десятичные эквиваленты шестнадцатеричных чисел.

Теперь представим себе, что будет, если для отображения текста в кодировке KOI-8 используется шрифт, настроенный на кодировку Win 1251. Пусть, например, в кодировке KOI-8 записана фраза «Кирилл и Мефодий». В компьютере ее будет представлять такая последовательность чисел:

EB (235), C9 (201), D2 (210), C9 (201), CC (204), CC (204), 20 (32), C9 (201), 20 (32), ED (237), C5 (197), C6 (198), CF (207), C4 (196), C9 (201), CA (202)

Числу EB (235) в кодировке KOI-8 соответствует буква К, числу C9 (201) – буква и и т.д. Но в шрифте, настроенном на кодировку Win 1251, числом EB (235) кодируется буква л, числом C9 (201) – буква Й. В результате получится такая фраза: ЛЙТЙММ Й нЕЖПДЙК

Такие превращения довольно характерны для русского Интернета. Часто, загрузив страницу текста из Интернета в браузер (специальную программу для просмотра публикаций в Интернете), можно увидеть мешанину из русских букв вместо понятного текста. Если такое случилось, попробуйте нужно просто изменить кодировку вручную. В разных браузерах это делается по-разному. В Internet Explorer 5.0 нужно в меню «Вид» раскрыть подменю «Вид кодировки» и выбрать команду «Кириллица (KOI8-Р)». После этого на экране появится нормальный русский текст. В подменю «Вид кодировки» представлены и другие кодировки.

Дата добавления: 2014-01-06