Передача имен процедур и функций в качестве параметров в подпрограммы

Вопросы для проверки знаний.

Begin

Begin

Begin

if n=1 then factorial:=1 else factorial:=n*factorial(n-1); {функция factorial(n) вызывает factorial(n -1) - саму себя}

end;

Пример 6. Программный код рекурсивной функции, вычисляющей числовую последовательность с рекуррентной формулой x ₁ = 3, x_n+1 = 4 x_n + 1 (строка 1 примера 2).

function seq (n: integer): integer;

if n=1 then seq:=3 else seq:=4*seq(n-1)+1; {функция seq(n) вызывает seq(n -1)}

end;

Пример 7. Программный код рекурсивно заданной функции из примера 4: F (0) = -3; F (n) = (n ² + 2 n - 3) × F (n -1) при (n > 0).

function r_fun (n: integer): integer;

if n=0 then r_fun:=-3 else r_fun:=(n*n+2*n-3)*r_fun(n-1);

end;

1. Какой способ задания числовых функций называют явным, а какой - рекуррентным?

2. Что называют рекуррентной формулой числовой последовательности (функции)?

3. Почему при задании рекурсии необходимо самое первое значение функции вводить присваиванием?

4. Какой способ вычисления значений функций называют рекурсией?

5. Может ли параметр числовой функции начинаться не со значения, равного 1?

6. Что необходимо определить при переходе от явного способа задания функции к рекуррентному?

7. Какие функции называют прямо рекурсивными, а какие - косвенно рекурсивными?

8. Как практически выполняется рекурсивный вызов функции, почему при его использовании необходимо учитывать емкость стека?

Практическое задание.

1. Разработать код рекурсивной функции, выполняющей возведение вещественного числа в целую степень.

Многие общие методы вычислительной математики, например, дифференциро­ва­ние (определение производных функции f (x) в заданной точке x = x ₀), интегрирование (расчет определенного интеграла функции f (x) на отрезке [ a, b ]) и др., формулируются таким образом, что применять их можно к самым различным функциям. При программной реализации данных методов возникает проблема передачи в подпрограммы, реализующие эти методы, имен процедур и функций в качестве их входных параметров. Например, при программной реализации общих методов дифференцирования и интегрирования наряду с входными параметрами x ₀ и a, b в соответствующие процедуры необходимо передавать и функцию f (x).

С этой целью в Паскале введены два особых типа данных - процедурный и функциональный. Их описания выполняют в разделе описания типов программы. Процедурный (функциональный) тип определяют в виде заголовка подпрограммы (процедуры или функции) со списком формальных параметров (который может быть пуст), но без имени самой подпрограммы.

Пример 1. Описание процедурного типа для процедур, у которых три вещественных входных параметра x,y,z и два вещественных выходных параметра a,b:

type Proc_type3r_2r = Procedure (x,y,z: real; var a,b: real);

Пример 2. Описание функционального типа для функций, у которых два вещественных входных параметра x,y и вещественный тип возвращаемого значения:

type Func_type2r_r = Function (x,y: real): real);

Пример 3. Описание процедурного типа для процедур без параметров:

type Proc_type = Procedure;

Фактически описание процедурного и функционального типа создает указатель на подпрограмму, которая после этого может определяться как переменная. После описания процедурных и функциональных типов их можно использовать для задания типов формальных параметров в заголовках других (внешних) подпрограмм.

Пример 4. Заголовок процедуры, у которой формальными входными параметрами являются процедура Pr и функция Fun, имеющие типы, заданные в примерах 1 и 2, а также задано два вещественных выходных параметра v,u:

рrocedure comp(Pr:Proc_type3r_2r; Fun:Func_type2r_r; var v,u: real);

Для практического использования внешних подпрограмм, в заголовки которых входят входные параметры-подпрограммы, необходимо дать описания реальных процедур и функций, имена которых будут передаваться как входные фактические параметры через вызовы внешних подпрограмм. Описания процедур и функций, выступающих в роли входных параметров внешних программ, должны компилироваться в режиме дальней адресации. Для этого в их заголовке указывается директива far или перед текстом описания подпрограммы задается ключ компиляции {$F+}. Он включает режим формирования дальнего типа вызова процедур и функций. После его использования выключить режим можно с использованием обратного ключа {$F-}. Прямой и обратный ключи вставляются в текст программы между описаниями подпрограмм.

Замечание. При подстановке фактических процедурных или функциональных параметров в вызов внешней подпрограммы в Free Pascal (в отличие от Турбо Паскаля) перед именем данных параметров необходимо ставить оператор адреса @.

Пример 5. Если в процедуру comp из примера 4 необходимо подставить процедуру Pr_1 типа Proc_type3r_2r и функцию F_2 типа Func_type2r_r, то при выходных параметрах a,b вызов процедуры comp в Free Pascal будет иметь вид:

comp(@Pr_1, @F_2,a,b);

Аналогичный вызов в Турбо Паскале будет иметь вид: comp(Pr_1, F_2,a,b).

Пример 6. Разработать две функции численного (приближенного) расчета первой и второй производных дважды дифференцируемой функции одного вещественного аргумента f (x) в заданной точке х = a с именами dfdx и d2fdx2. Для приближенного расчета производных использовать разностные отношения:

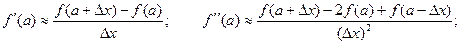
где D х – заранее заданное малое положительное число. В функциях принять: D х = 0,001.

Вычисление дифференцируемой функции f (x) реализовать с помощью функции F1(x), имя которой передается как параметр. В качестве реальной функции f (x) для отладки программы принять sin(0,5 x).

Значение точки х = a вводится в программу с клавиатуры, рассчитанные функциями dfdx и d2fdx2 приближенные значения первой и второй производных в точке х = a выводятся на экран.

Решение. Введем в основной программе глобальный параметр x0 – вводимое число. В описаниях типов введем тип Fun, который представляет собой функцию от одного вещественного аргумента, возвращающую вещественное значение.

Программный код с необходимыми комментариями:

type Fun = function(x: real): real; {описание функционального типа}

var x0: real;

{$F+} { включение режима дальнего типа вызова процедур и функций}

Function F1(x: real): real; {описание функции - фактического параметра}

begin F1:= sin(0.5*x) end;

{$F-} {выключение режима дальнего типа вызова процедур и функций}

Function dfdx (F:Fun; x:real):real; {описание функции для расчета первой производной}

begin dfdx:=(F(x+0.001)-F(x))/0.001; end;

Function d2fdx2(F:Fun;x:real):real; {описание функции для расчета второй производной}

begin d2fdx2:=(F(x+0.001)-2*F(x)+F(x-0.001))/0.000001; end;

begin {открытие основной программы}

WriteLn(' Vvedite x0:'); Read(x0); {запрос на ввод и ввод значения аргумента x0 }

WriteLn(' First derivative of function at',x0:10,'=',dfdx(@F1,x0):10);

WriteLn(' Second derivative of function at',x0:10,'=',d2fdx2(@F1,x0):10);

Дата добавления: 2014-01-06