Критерии качества переходного

.

Апериодическое звено второго порядка

Дифференциальное уравнение

.

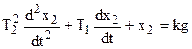Характеристическое уравнение и его корни

Апериодическое звено второго порядка имеет действительные корни характеристического уравнения. Для этого должно выполняться условие

.

Вставить переходную и весовую функцию.

При выполнении этого условия характеристическое уравнение может быть представлено в виде произведения

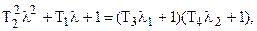
причем постоянные времени T3 иT4 находятся из уравнений

.

Передаточная функция апериодического звена второго порядка

может быть представлена как произведения передаточных функций двух апериодических звеньев с общим коэффициентом усиления k:

.

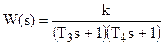Амплитудно-фазовая частотная характеристика получается, если положить s=jw:

.

Частотную передаточную функцию можно представить в виде

W(jw)=U(w)+jV(w).

Из полученного выражения следует, что

- при w=0 и при w=¥ W(jw)=0,

- при w=1/(T₃T₄)^-1/2 действительная часть Re[W(jw)]=0 и фазовый сдвиг в системе на этой частоте равен -p/2,

- при w>1/(T₃T₄)^-1/2 действительная (U(w)) и мнимая (V(w)) части передаточной функции отрицательны и, следовательно, фазовый сдвиг в апериодическом звене второго порядка j(w)<p/2 (годограф при wt ®¥ проходит через третий квадрант).

По этим данным можно качественно определить вид амплитудно-фазовой частотной характеристики звена (рис. 3).

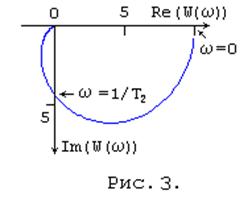
Амплитудно-частотная, амплитудная и фазовая частотные характеристики звена - произведение амплитудных частотных характеристик двух апериодических звеньев:

,

.

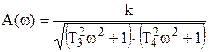Сопрягающие частоты, полагая для определенности, что T₃>T₄, w₁=1/T₃, ₂=1/T₄. При w=(w₁w₂)^1/2=1/T₂ то есть на среднегеометрической частоте, j()=-90^o. Максимальный фазовый сдвиг lim_w®¥j(w)=-180^o.

Выделение апериодическое звено второго порядка как отдельного типового звена оправдано тем, что в ряде случаев физически - это один элемент САУ (например, два сообщающиеся объема, наполняемых газом под давлением, электрический двигатель постоянного тока и др.).

Дата добавления: 2014-01-06