Устойчивость САУ

Необходимым, но не достаточным, условием устойчивости САР является положительность всех коэффициентов характеристического уравнения системы (если все коэффициенты отрицательны - умножением на минус единицу их можно сделать положительными). Если не все коэффициенты положительны, то система неустойчива и никакие дополнительные исследования не требуются.

Это условие является достаточным для систем первого и второго порядка.

Определение устойчивости линейной невозмущенной системы, то есть системы, при нулевом входном сигнале (g(t)º0).

Линейная невозмущенная система ([29], стр. 60):

Система устойчива, если при конечном начальном отклонении выходной сигнал остается ограниченным для любого t>0:

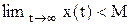, где M – некоторая положительная постоянная величина.

Под начальным отклонением понимаются ненулевые начальные условия системы.

Система асимптотически устойчива, если при конечном начальном отклонении выходной сигнал с течением времени обращается в нуль:

.

Система неустойчива, если при произвольно малых начальных отклонениях, выходной сигнал с течением времени неограниченно растет:

.

Интегрирующее звено сохраняет начальное отклонение. Это звено устойчиво, но не асимптотически устойчиво.

Система, возмущенная действием входных сигналов из заданного множества, устойчива, если выходной сигнал остается ограниченным для всех сигналов этого множества.

Под действием постоянного, отличного от нуля, сигнала на входе интегратора (g(t)=const) сигнал на его выходе неограниченно возрастает. Такой сигнал не должен входить в заданное множество.

Определения устойчивой системы и асимптотически устойчивой системы можно объединить ([1], с. 84) одним определением, если рассматривать не координату системы, а только собственное (свободное) движение системы:

Под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени.

Если x(t) - решение уравнения, описывающего свободное движение системы:

,

то для устойчивой САУ x_собств (t)®0 при t®¥.

Необходимое условие устойчивости - положительность всех коэффициентов характеристического уравнения. При n³3 оно недостаточно. Как будет показано ниже на ряде примеров уже САУ третьего порядка (n=3) может оказаться неустойчивой и при положительных коэффициентах дифференциального уравнения.

Если l_i = a_i + w_i (i=1…n) - корни характеристического уравнения

,

то система устойчива, если корни характеристического уравнения расположены в левой полуплоскости комплексного переменного l (a_i < 0).

Это очевидно (если нет кратных корней) из равенства

.

Следуя [7], будем называть такой многочлен устойчивым.

1. Критерий Гурвица [5]

Исторически этот критерий появился первым (1875 - Раус, 1895 - Гурвиц). Задача состояла в том, чтобы, не вычисляя корни характеристического уравнения, что при отсутствии вычислительной техники и при высокой степени уравнения сложно, найти условия устойчивости характеристического многочлена.

Приводится без доказательства.

Из коэффициентов многочлена составим квадратную матрице размера n×n (так называемую матрицу Гурвица [3]), по следующему правилу

По диагонали выписываются коэффициенты характеристического уравнения, начиная с a₁. Строки матрицы заполняются коэффициентами: влево от диагонали записываются коэффициенты с возрастающими индексами, а справа - с убывающими. Остальные элементы матрицы - нули.

Ниже представлена матрица для n=6 (a₀>0):

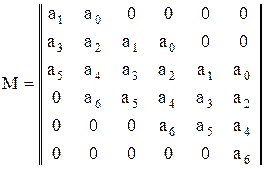
В первой строке слева места нет, а с меньшим индексом всего один коэффициент a₀. В последней строке коэффициентов с возрастающими индексами нет, а для коэффициентов с убывающими индексами справа нет места.

В литературе встречается и правило составления транспонированной матрицы [1].

Из матрицы образуют так называемые определители Гурвица - главные диагональные миноры матрицы:

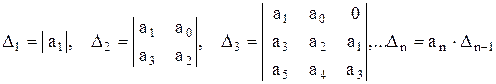
Формулировка критерия:

Для устойчивости системы необходимо и достаточно, чтобы a₀>0 и определители Гурвица были положительными.

Заметим, что при вычислении каждого последующего определителя используются уже вычисленные значения предыдущих определителей. Это сокращает объем вычислений.

Пример.

Пусть передаточная функция разомкнутой системы

.

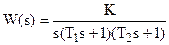Передаточная функция замкнутой системы:

Тогда дифференциальное уравнение свободного движения системы после ее замыкания

.

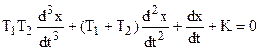Следовательно, a₀=T₁T₂; a₁= (T₁+T₂); a₂=1; a₃=K.

Матрица Гурвица системы третьего порядка:

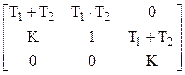
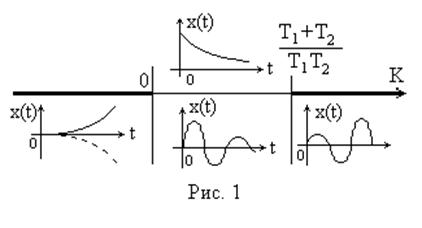Условие a₀>0 выполняется и, следовательно, D₁= T₁+T₂>0. Условие

D₂= T₁+T₂-KT₁T₂>0 равносильно условию .

Третий определитель D₃=KD₂, что равносильно условию K>0. Таким образом, усиление системы должно лежать в пределах (рис. 1)

0< .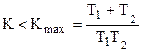

При K<0 в обратная связь положительная, а при K>K_max теряется устойчивость. На рис.1 изображены переходные процессы в системе при различных коэффициентах усиления системы.

Недостатки критерия:

- в случае неустойчивости системы критерий не дает ответа на то, как нужно изменить параметры системы, чтобы сделать ее устойчивой;

- в случае устойчивой системы критерий не дает информации о качестве регулирования и о запасах устойчивости.

В силу этих обстоятельств в инженерной практике чаще используются более удобные с этой точки зрения критерии.

Дата добавления: 2014-01-06