Гармоническая линеаризация типовых звеньев

Введение в теорию нелинейных САУ

(по Попову “Динамика...”, стр. 92)

Устойчивость линейных САУ определяется знаком вещественных частей корней характеристического уравнения и не зависит от начальных условий. Если линейная система устойчива, то переходный процесс затухает.

В нелинейных системах:

- сам факт затухания или расхождения процесса зависит не только от параметров системы, но и от начальных условий;

- затухание процесса может происходить не до нуля, а расхождение не до бесконечности, при этом может изменяться общий характер протекающего в системе процесса (например, частота свободных колебаний, колебательный процесс может превратиться в апериодический и наоборот и т.п.);

- может иметь место неоднозначность установившегося состояния даже при отсутствии внешних воздействий.

Поэтому при анализе устойчивости нелинейной САУ необходимо оговаривать:

- относительно какого устойчивого состояния исследуется устойчивость системы (равновесного или периодического и какого именно);

- ограничения на рассматриваемые при анализе начальные условия.

Нелинейные звенья с однозначными и симметричными относительно начала координат характеристиками не вносят сдвига фаз первой гармоники, то есть для таких элементов q₂(a) º 0.

На рис.1 представлены характеристики нескольких часто встречающихся нелинейных звеньев.

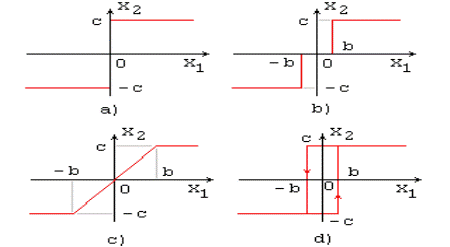
Рис.1

Таблица

Тип звена	q1(a)	q2(a)
Идеальное релейное (Рис.1a)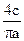
Релейное с зоной не чувствительности (Рис.1b)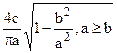
Насыщение (Рис. 1с)
Релейное с петлей гистерезиса (Рис1d)

В таблице приведены зависимости коэффициентов гармонической линеаризации некоторых нелинейных звеньев от амплитуды входного сигнала (a). На рис.2 представлены графики этих зависимостей q_i(a) (i=1,2) для идеального реле (рис.2a),для реле с зоной нечувствительности (рис.2b) и для реле с петлей гистерезиса (рис.2c и 2d) при параметрах нелинейностей b=1,c=1.

Рис.2

Часто оказывается необходимым учитывать нелинейности типа дискриминатора (например, при исследовании так называемый срывов слежения).

Расчет автоколебаний по критерию Найквиста.

Ограничимся случаем, когда передаточная функция нелинейности зависит только от амплитуды сигнала (вообще говоря, это не всегда так).

Передаточная функция по первой гармонике:

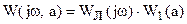
Система находится на границе устойчивости, т.е. в ней возможны незатухающие колебания, если для некоторой частоты (частоты автоколебаний) выполняется условие

.

Задаваясь различными значениями амплитуды первой гармоники (a) строим амплитудно-фазовую характеристику системы (годограф Найквиста). При некотором значении амплитуды (a = a1) при некоторой частоте (w = w1) годограф проходит через точку (-1, 0). Следовательно, в системе будут автоколебания на частоте w1 с амплитудой a1.

Остаются открытыми вопросы об устойчивости этих колебаний (не будет ли амплитуда увеличиваться с течением времени, т.е. устойчив ли соответствующий замкнутый цикл на фазовой плоскости), о существовании других решений и т.д.

Пример.

Нелинейность типа идеальное реле с выходным сигналом ±1

9) Пространство состояний (фазовое пространство)

Вектор состояния состоит из компонент выбранных так и в таком количестве, что если известно их (компонент) значения в момент времени t=0 при заданном входном воздействии, то выходной сигнал оказывается однозначно определенным.

Пространство состояний – N-мерное пространство, координатами которого служат переменные состояний.

Траектория состояний – геометрическое место точек конца вектора состояния в пространстве состояний в течение некоторого отрезка времени.

Если входное воздействие равно нулю, то траектория состояний описывает свободное движение системы. Портрет состояний системы – траектория невозмущенного движения системы.

Фазовое пространство системы – это пространство состояний, координаты которого производные по времени.

Можно определить

Непрерывные (аналоговые) системы – системы вектор состояний которых изменяется непрерывно в пространстве состояний. Пространство состояний при этом может быть ограниченным или неограниченным. Обычно оно ограничено физическими ограничениями на компоненты вектора состояний.

Цифровые системы – системы вектор состояний которых может принимать лишь определенные значения из конечного (обычно) счетного множества возможных состояний.

Фазовая плоскость - плоскость, на которой по двум осям откладываются какие-либо две переменные, характеризующие поведение системы в динамике (в переходном процессе). Наиболее распространенный выбор координат - регулируемая величина x и ее производная по времени (скорость) v = dx/dt, как показано на рисунке.

При таком выборе координат существуют правила, которые надо учитывать при построении фазового портрета:

- В верхней полуплоскости (dx/dt >0) изображающая точка всегда движется слева направо (в сторону увеличения x),

- В нижней - справа налево (в сторону уменьшения x);

- Фазовые траектории пересекают ось 0x под прямымуглом. Это следствие того, что в точке пересечения dx/dt = 0, а величина x(t) достигает экстремального значения.

Пусть задано уравнение

.

Введя обозначения 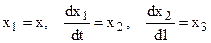, получим систему уравнений в нормальной форме (форме Коши):

Теперь можно образовать трехмерное фазовое пространство с координатами (x₁, x₂, x₃), которые полностью определяют состояние системы.

Уравнение можно записать в матричном виде:

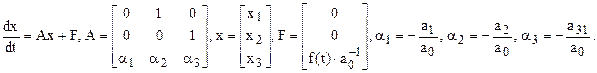
Отметим, что здесь x= (x₁, x₂, x₃)^T - вектор.

Матричной записи дифференциального уравнения можно поставить в соответствие и матричную запись решения с начальными условиями x(t₀)=C₀:

Мнемоническое правило обозначения переменных при приведении уравнения n-ного порядка к нормальной форме (Иванов и др. с.131):

x1	x2	x3	…..	xn
x	dx/dt	d^2x/dt^2	…..	dx^(n-1)/dt^(n-1)

В линейных системах переходный процесс может или затухать (в устойчивых системах) или расходится независимо от начальных условий. В нелинейных системах возможны автоколебания с постоянной амплитудой и частотой. Такая система неустойчива относительно равновесного состояния.

Нестрогое определение устойчивости нелинейной системы.

Если амплитуда колебаний мала, их частота приемлема, то систему считают практически устойчивой. Обычно требуется, чтобы частота собственных колебаний была выше основной частоты управляющего воздействия (во избежание возникновения низкочастотных биений с разностной частотой) и не вызывала бы в системе нежелательных физических процессов (например, перегрева электродвигателя, вызываемого его частым реверсированием в процессе автоколебаний и т.п.).

Если амплитуда колебаний неприемлема для целей регулирования, то САУ практически неустойчива.

Характерные признаки автоколебаний практически устойчивой нелинейной системы:

Автоколебания являются собственными свободными колебаниями системы.

Амплитуда и частота автоколебаний не зависят от начальных условий, а зависят только от параметров системы.

Параметры автоколебаний устойчивы при изменениях параметров системы в достаточно широких пределах.

Гистерезис – это свойство звена, когда его состояние определяется не только условиями на его входе в данный момент времени, но и условиями, существовавшими в предшествующие моменты.

Иными словами – отставание следствия от производящей его причины вследствие существовавших ранее условий.

Нелинейные системы существенно богаче по своим возможностям и разнообразию свойств, чем

САУ с идеальным реле и жесткой обратной связью

Структурная схема системы представлена на рис. 3. Частотная передаточная функция линейной части системы W(p), где p=d/dt – символ дифференцирования.

Нелинейное звено – идеальное реле. Полагая входной сигнал g тождественно равным нулю, получим

Введя обозначение dx/dt=y, получим

Отношение этих выражений не содержит в явном виде времени и определяет фазовый портрет системы:

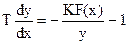
При заданной функции F(x) задача построения фазовой траектории сводится к решению двух уравнений

.

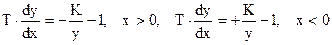Решения могут быть найдены в замкнутом виде.

Качественная картина приводится.

Дифференциальное уравнение изменяется при изменении знака F(x) на так называемой линии переключения. В данном случае линия переключения x=0 совпадает с осью ординат. По мере стягивания траектории к началу координат амплитуда колебаний неограниченно уменьшается, а частота – неограниченно возрастает.

Если реле имеет петлю гистерезиса, то возникает предельный цикл колебаний

Дата добавления: 2014-01-06