Реле с петлей гистерезиса

Нахождения частоты и амплитуды автоколебаний в САУ, состоящей из реле с гистерезисной петлей и инерционного интегрирующего звена м етодом приравнивания нулю годографа Михайлова.

Пусть линейная часть разомкнутой САУ имеет частотную передаточную функцию

,

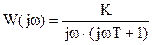
а гармонический коэффициент передачи нелинейного звена

W_н(a)=q₁(a)+jq₂(a),

a - амплитуда автоколебаний.

Передаточная функция разомкнутой системы

,

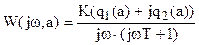Характеристическое уравнение замкнутой САУ – сумма многочленов, стоящих в знаменателе и числителе передаточной функции:

Ф(jw,a)= -w²T+jw+Kq₁(a)+jKq₂(a).

Система находится на грани устойчивости, если годограф Михайлова проходит через начало координат. Приравнивая нулю действительные и мнимые части уравнения Ф(jw,a)=0, получим систему уравнений, из которой можно определить амплитуду (a) и частоту (w) автоколебаний:

-w²T+Kq₁(a)=0

w+Kq₂(a)=0.

Для реле с петлей

.

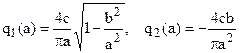Подставляя из второго уравнения w=-Kq₂(a) в первое, получим

.

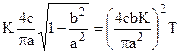После простейших преобразований получим

,

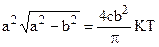После возведения в квадрат обоих частей равенства и введения относительной амплитуды a=a/b, получим кубическое уравнение относительно a²:

.

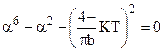Действительный корень этого уравнения и определяет амплитуду автоколебаний. В таблице приведены действительные корни для нескольких значений

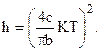
Таблица

h		0.25	0.5
a		1,086	1,139	1,211	1,3	1,365	2,336

Построение фазового портрета САУ с реле с зоной нечувствительности.

(Иващенко Н.Н. стр.488)

Дифференциальное уравнение системы:

.

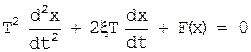Если положить в уравнении F(x)=X_c постоянной величине (т.е. рассмотреть движение системы при постоянном возмущении), то решение уравнения

,

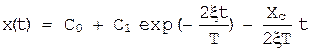где С₀ и C₁ - постоянные интегрирования, зависящие от начальных условий, -X_c t/2xT - вынужденное движение системы под действием постоянного возмущения X_c. В установившемся режиме вторая производная обращается в ноль и система продолжает движение с постоянной скоростью. (Выгодский М.Я. Справочник по математике. М.; Физматгиз, 1962, с. 743)

Представим уравнение в виде системы уравнений первого порядка. Для этого обозначим dx/dt=v. Тогда
получим

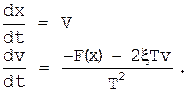
Нелинейную функцию определим как

F(x)= c при x>b,

F(x)= 0 при ½x½£b,

F(x)= -c при x<-b.

Исключим из системы уравнений время t для чего разделим второе уравнение на первое:

Уравнение изоклин, то есть геометрического места точек на котором производная dv/dx=С

.

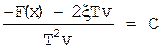Определим значение производной dv/dx при ½x½£b. Так как на зтом интервале F(x)º 0, то

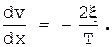
Интегрируя полученное дифференциальное уравнение, получим

,

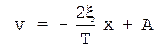где A - постоянная интегрирования. Задавая различные значения постоянной интегрирования, получим множество отрезков прямых с отрицательным наклоном к оси 0x (Рис.1). Это и есть изоклины фазовой траектории на данном интервале изменения координаты x.

Найдем уравнение изоклины, на которой dv/dx=¥. Очевидно, что уравнение изоклины v=0, то есть все фазовые траектории при v=0 имеют касательные параллельные оси 0x.

Уравнение изоклины, на которой dv/dx=0

-F(x)-2xTv₀=0.

Откуда

.

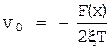Поскольку F(x) может принимать только значения F(x)=c и F(x)=-c, то в верхней полуплоскости уравнение изоклины v₀=c/2xT, в нижней - v₀=- c/2xT.

Это совпадает с полученным выше установившимся значением скорости при постоянном воздействии.

Из этого следует, что при вхождении в зону нечувствительности (b и -b на рис.1) со скоростью v₀ пересечение изображающей точкой линии переключения происходит под углом 90 градусов (Рис.2).

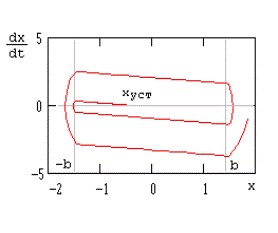
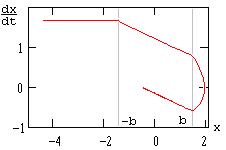
Если система устойчива, то движение прекращается в одной из точек зоны нечувствительности (точка x_уст на рис.1). В неустойчивых системах образуется устойчивый цикл.

Решение дифференциального уравнения

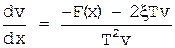
для F(x)=±c может быть получено в замкнутом виде. По полученным зависимостям v=v(x,c) и v=v(x,-c) могут быть построены траектории движения изображающей точки вне зоны нечувствительности. В общем случае получить решение уравнения

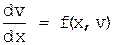
в замкнутом виде не удается. Для построения фазовых портретов можно использовать метод изоклин или интегрировать дифференциальное уравнение численно.

Дата добавления: 2014-01-06