Прямые и обратные разности

Дополнение.

Представив сигнал в экспоненциальной форме, получим сразу

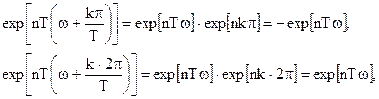
Это и показывает, что

- Входные сигналы одинаковой амплитуды, имеющие частоты симметричные относительно частоты w_T/2 после дискретизации с периодом T дают решетчатые функции, которые отличаются только знаком. Поэтому достаточно изучать свойства ДВ-систем на интервале частот от нуля до w_T/2.

- В ДВ-системах невозможно различить две частоты, разность между которыми dw= k×2p/T, k - целое.

Для решетчатых функций определены понятия аналогичные производной и интегралу для непрерывных функций. Аналог первой производной непрерывной функции для решетчатой функции является либо первая прямая разность [5].

Df[n]=f[n+1]-f[n]

либо первая обратная разность

Ñf[n]=f[n]-f[n-1].

Выражение для обратной первой разности легко получить заменой в прямой первой разность n на n-1.

Для определения прямых разностей требуется знание текущего значения решетчатой функции (f[n]) и ее будущих значений. Обратные разности, в отличие от прямых, требуют для определения текущего значения решетчатой функции и ее прошлых значений (f[n-m], m>0). Поскольку в большинстве практических задач будущие значения неизвестны, в дальнейшем, будем рассматривать обратные разности.

Вторые разности (аналог второй производной непрерывной функции)

Ѳf[n]= Ñf[n]- Ñf[n-1].

Развернутое выражение для обратной второй разности:

Ѳf[n]= Ñf[n]- Ñf[n-1]={f[n]-f[n-1]}-{f[n-1]-f[n-2])=f[n]-2f[n-1]+f[n-2].

В общем виде для прямые и обратные разности k-го порядка вычисляются по формулам [5]

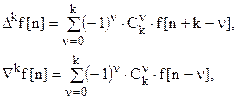
C_kⁿ - биномиальные коэффициенты.

Если f[n] º0 при n<0, то в точке n=0 обратная разность любого порядка (k>0)

.

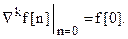Неполная сумма 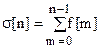и полная сумма 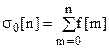- аналоги интеграла непрерывной функции. Разница между ними в том, что в полную сумму входит и f[n].

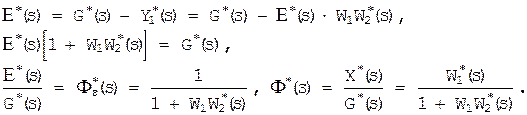
F_e^*(s)- передаточная функция замкнутой чисто импульсной системы по ошибке, F^*(s) - передаточная функция замкнутой чисто импульсной системы по сигналу. Соответствующие частотные передаточные функции получается заменой в частотных передаточных функциях s на jw.

Существует большое разнообразие структурных схем ДВ-систем, отличающихся местом включения импульсных элементов и передаточными функциями.

Дата добавления: 2014-01-06