
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия. Л 5 . Модели финансовой математики
|
|
|
|
Л 5. Модели финансовой математики.
Практически до середины XX века финансовая математика оперировала лишь понятиями простого и сложного процентов в рамках расчетов приведенной (текущей) стоимости финансовых потоков. Отмена золотого стандарта, инициировавшая появление большого количества новых финансовых инструментов и приемов, включая фьючерсные сделки, породила значительный рост этого раздела математики на основе вероятностно-статистических методов.
В России финансовая математика представляла до последнего времени интерес только для части специалистов банковского дела и не входила в широкий обиход. Подобная безграмотность общества послужила одной из причин появления большого количества финансовых пирамид и существенных затруднений в становлении банковского дела в плане доверия к нему со стороны населения. В настоящее время финансовой математики являются, на наш взгляд, предметом общей культуры, что объясняет появление данного раздела в пособии.
В современном мире деньги рассматривается в качестве обычного товара, пользование которым определенный срок времени подлежит оплате пропорциональной сумме заема. Так появляется понятие процентной ставки, связанной с базовой единицей времени, например, 5 % годовых. Кроме того, в подобных операциях устанавливается период конвертации процентов к заемному капиталу, в конце которого процентный доход приходуется. Процентная ставка называется фактической, если период конвертации совпадает с базовой единицей времени и номинальной в противном случае. В этих условиях появляется схема сложных процентов.
Пусть r - фактическая годовая процентная ставка. Положим для простоты, что она постоянна во времени. В этом случае ее называют технической. Теперь нетрудно рассчитать, используя понятие сложного процента, текущее значение капитала S, переданного в заем на n=1,2,…лет при фактической процентной ставке r
S(1+ r), S(1+ r 2), …, S(1+ r)n,…
Степени числа (1+ r) называют накопительными множителями. С ними тесно связано понятие дисконтирующего множителя
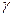 =
= 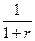 ,
,
позволяющего вычислить данную (текущую) стоимость выплаты суммы S через n=1,2,… лет
S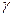 , S
, S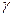 2, …,S
2, …,S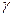 n,…
n,…
Простейшими видами финансовых потоков являются бессрочные ренты и аннуитеты. Рассмотрим для простоты бессрочную ренту, представляющую поток выплат величины 1 в конце каждой базовой единице времени с первой выплатой в момент времени 0 (рента пренумерандо).Текущая (приведенная) стоимость такой ренты представляет величину
1+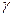 +
+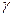 2+…=
2+…=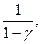
как сумму бесконечной геометрической прогрессии.
Для аннуитета, являющегося последовательностью конечного числа n выплат в конце последовательных базовых единиц времени с первой выплатой в момент времени 0, справедлива аналогичная формула
1+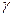 +
+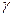 2+…
2+…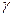 n-1 =
n-1 = 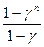
Кроме основных банковских операций приведенные формулы широко используются в моделях страхования жизни и пенсионных схемах.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 239; Нарушение авторских прав?; Мы поможем в написании вашей работы!