Портфель инвестиций

Далее рассматривается проблема инвестиций (вложения) собственных средств инвестором в существующие финансовые активы (твердые валюты, акции, облигации и пр.), а не только банковского вклада и заема. Обратимся к случаю краткосрочного вложения, для которого вопросы дисконтирования не представляют существенного интереса. Здесь на первый план выходят показатели доходности и рисковости для каждого отдельного финансового актива.

Назовем портфелем инвестиций в активы 1,2,…, m доли собственных средств

, , …, ,

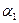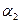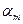вложенных инвестором в соответствующие активы. Очевидно, что

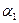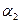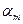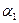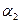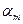, , …, ≥ 0, + + …+ =1.

Используя идеи Г.Марковица, будем характеризовать будущие доходности активов в очередной период времени случайными величинами

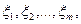
образующими случайный вектор 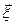со средним значением

М()=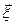

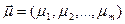
и ковариационной матрицей

,

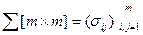диагональные элементы которой являются дисперсиями величин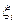

,

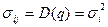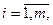
а недиагональные – коэффициентами ковариации для величин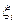и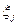

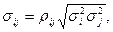
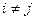
Здесь коэффициент 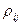является коэффициентом корреляции между величинам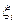ии .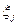

Вкладывая долю 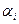средств в 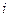^ый актив 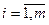, мы имеем портфель инвестиций

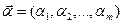
со средней доходностью

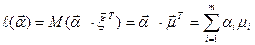
неосторожный инвестор, ориентируясь только на среднюю доходность, фактически решает оптимизационную задачу

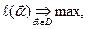(1)

где 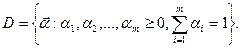Решение 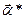задачи (1) легко находятся. Пусть

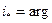max ,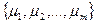

тогда

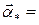(0,0,…,0,1 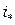,0,…,0)

Это означает, что все наличные средства неосторожный инвестор вкладывает в актив, имеющий максимальную доходность, если такой актив единственен.

Порочность такого варианта планирования подтверждается существующей практикой. Ориентируясь только лишь на среднюю доходность акций, сотни тысяч наших сограждан стали жертвами многих финансовых пирамид. Опасность подобного подхода связана с полным игнорированием рисковости вложения - непременным атрибутом расчетов осторожного инвестора. Проблема состоит в способе измерения риска. Согласно основной идеи Г.Марковица риск стоит измерять дисперсией случайной доходности 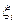i^го актива (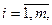) в будущий период времени. Таким образом, рисковость портфеля 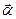можно измерять величиной дисперсии случайной доходности 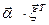портфеля

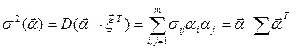(2)

Теперь, осторожный инвестор, не обращающий внимания на среднюю доходность, может конструировать наименее рисковый портфель, решая оптимизационную задачу

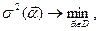
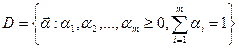
где
Эта нелинейная задача может быть решена методами квадратичного программирования. Приведем ее решение для случая двух активов (m = 2). В этом случае целевая функция (2) является функцией одного переменного 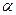, если ввести переобозначения

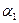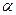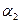=, =1-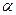

Запишем функцию (2) в развернутой форме

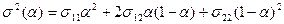(3)

Безусловная точка минимума функции (3) находится методом дефферинциального исчисления. Возьмем производную от функции (3)

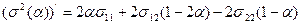
и приравняем ее к нулю. Решением полученного уравнения будет величина

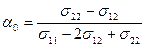
Теперь, реализуя условия 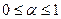, находим искомое.

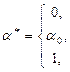
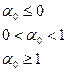
Исследуем качественное поведение минимума функции (3). Для этого представим ее в форме

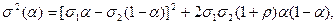
которая показывает, что теоретически рисковость портфеля может равняться нулю, т.е. портфель окажется безрисковым, если коэффициент корреляции между активами равняется -1. Этот результат имеет практическое значение в том случае, когда у инвестора имеется возможность выбора пары активов. Именно, среди доступных всевозможных пар активов можно искать пару, обладающую минимальным коэффициентом корреляции.

В общем случае m активов, когда инвестора интересует и средняя ожидаемая доходность портфеля, выражаемая функцией 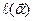и рисковость - представимая функцией 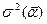, мы имеем дело с двухкритериальной задачей, решение которой проводится приемами, отмеченными выше. Либо инвестор фиксирует доходность портфеля на допустимом уровне 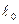и решает оптимизационную задачу

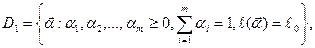
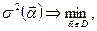
где

либо строит множество недоминирующих друг друга портфелей (множество Парето).

Дата добавления: 2014-01-06