Формула полной вероятности. Пусть событие может наступить при условии появления одного из несовместных событий , которые образуют полную группу

Пусть событие 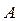может наступить при условии появления одного из несовместных событий 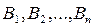, которые образуют полную группу. Пусть известны вероятности этих событий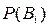 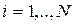и условные вероятности .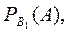

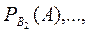
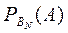Теорема. Вероятность события 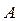, которое может наступить лишь при условии появления одного из несовместных событий 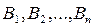, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события :

-

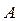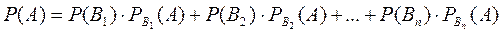- формула полной вероятности.

Доказательство. По условию, событие 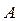реализуется лишь при осуществлении любого из несовместных событий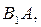 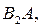…,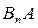. Тогда по теореме сложения

. (*)

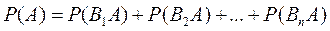Каждое слагаемое в этой формуле по теореме умножения вероятностей зависимых событий:

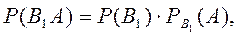
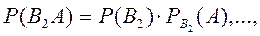
Подставляя эти формулы в (*) получим формулу полной вероятности.

Пример. Имеются три урны с шарами. В первой находится 5 голубых и 3 красных шара, во второй – 4голубых и 4 красных, в третьей – 8 голубых. Наугад выбирается одна из урн и из нее наугад извлекается шар. Какова вероятность того, что он окажется красным (событие ).

Решение. Шар может быть извлечен из любых трех урн. Обозначим через - выбор урн. Вероятности выбора урн одинаковые: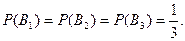Из условия задачи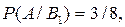

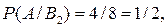
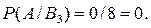
Тогда искомая вероятность

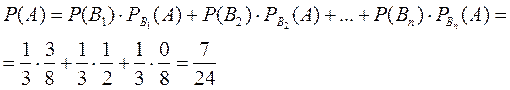
3. Вероятность гипотез. Формула Бейеса

Пусть событие 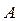может наступить при условии появления одного из несовместных событий 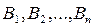, образующих полную группу. Так как заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность наступления события 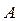определяется по формуле полной вероятности

.

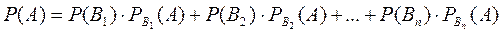Допустим, что произведено испытание, в результате которого появилось событие 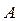. Поставим себе задачу, определить, как изменились в связи с наступлением события 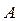, вероятности гипотез 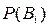, т.е., , ?

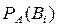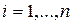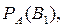
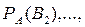
Найдем условные вероятности 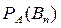по теореме умножения вероятностей

.

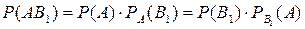Отсюда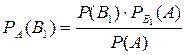

или .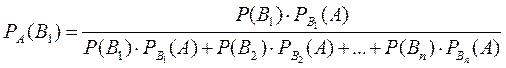

Аналогично выводятся условные вероятности остальных гипотез

.

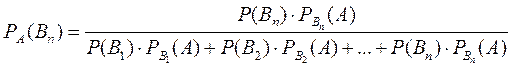Это формулы Бейеса, позволяющие переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие .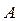

Пример. В пяти ящиках находятся одинаковые по весу и размерам ящиках шары. В двух ящиках – 6 голубых и 4 красных шара (ящик состава 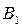). В двух других ящиках (состава 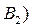- по 8 голубых и 2 красных шара. В одном ящике (состава 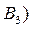- 2 голубых и 8 красных шаров. Наудачу выбирается ящик и из него извлекается шар. Извлеченный шар оказался голубым. Какова вероятность того, что голубой шар извлечен из ящика первого состава?

Решение. Обозначим через 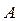событие, состоящее в том, что голубой шар извлечен из ящика первого состава?

Из условия задачи

.

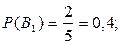
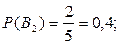
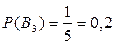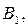
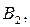
Вероятности вынуть голубой шар, если известно, что взяты ящики состава 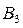соответственно:

;

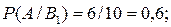
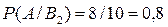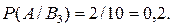
В соответствии с формулой полной вероятности: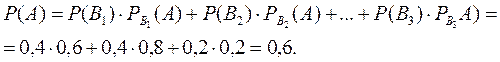

По формуле Бейеса найдем искомую вероятность

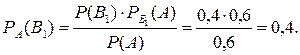
Глава 5. Повторение испытаний

Дата добавления: 2014-01-06