Формула для вычисления дисперсии

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

.

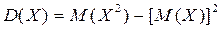Доказательство. Принимая во внимание, что математическое ожидание 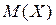есть величина постоянная, следовательно, постоянны и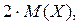 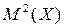. Упростим формулу, выражающую определение дисперсии:

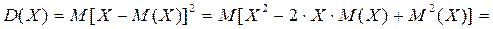
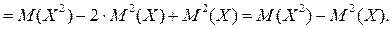
Итак .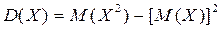

Пример. Найти дисперсию случайной величины , которая задана законом распределения

2 3 5

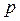
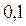
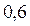
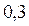
Решение. Найдем математическое ожидание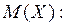

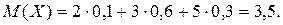
Напишем закон распределения случайной величины :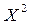

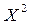4 9 25

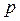
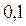
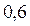
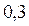
Найдем математические ожидания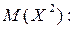

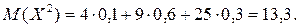
Искомая дисперсия

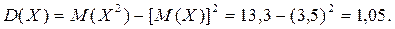
5. Свойства дисперсии

Св-во 1. Дисперсия постоянной величины 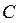равна нулю.

Доказательство. По определению дисперсии,

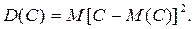
Пользуясь свойством математического ожидания о том, что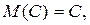

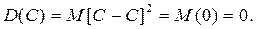
Итак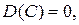

т.е. постоянное число рассеяния не имеет.

Св-во 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

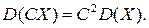
Доказательство.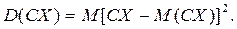

Пользуясь свойством математического ожидания о том, что 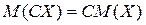, получим 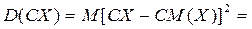и ь величина постоянная, следовательно постоянны анием квадрата случайной величины отклонения на их вероятности.

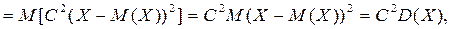
т.е.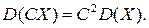

Св-во 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

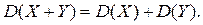
Доказательство. По формуле для вычисления дисперсии 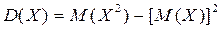имеем .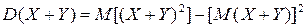

Раскрыв скобки и пользуясь свойствами математического ожидания, т.е.

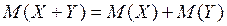
получим

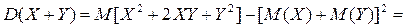
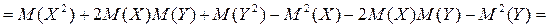
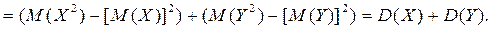
Получили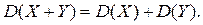

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Например, для трех слагаемых имеем

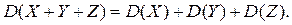
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

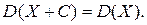
Доказательство. Величины 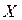и 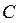независимы, поэтому

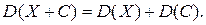
Так как 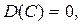то

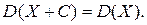
4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

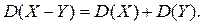
Доказательство. В силу третьего свойства дисперсии 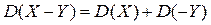и учитывая, что ,

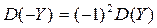Получим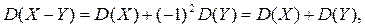

т.е.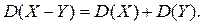

Дата добавления: 2014-01-06