Работа, мощность,кинетическая энергия

Работа силы.

Пусть частица под действием силы 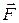совершает перемещение по некоторой траектории (рис.1.6.1). Рассмотрим элементарное перемещение 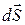, в пределах которого силу можно считать постоянной.

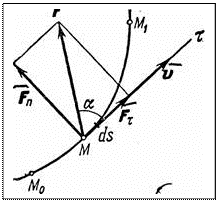Действие силы на перемещении 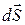можно характеризовать величиной, равной скалярному произведению силы и перемещения, которую называют элементарной работой силы 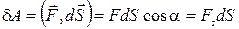, (1.6.1)

где - угол между векторами силы и перемещения, 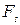- проекция силы на перемещение. Работа – величина алгебраическая, т.е. она может быть как положительной, так и отрицательной в зависимости от величины . Работа может быть также равна нулю, если сила перпендикулярна перемещению.

Необходимо отметить, что бесконечно малая работа не является полным дифференциалом: в общем случае она зависит от траектории.

Суммируя выражение (1.6.1) по всем элементарным участкам пути, найдем работу силы на данном пути:

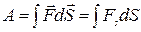. (1.6.2)

Укажем, что формула (1.6.2) справедлива не только для частицы, но и для любого тела. В этом случае 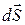- перемещение точки приложения силы.

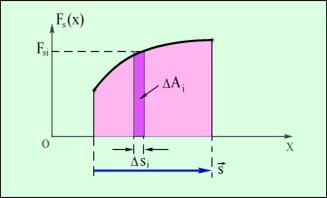
Рис.1.6.2.

Выражению (1.6.2) можно придать наглядный геометрический смысл. Изобразим график 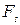как функцию положения частицы на траектории (рис.1.6.2). Из рисунка видно, что элементарная работа численно равна площади выделенной полоски, а работа на всем пути – площади фигуры, образованной линией графика и осью . При этом площадь фигуры над осью берется со знаком плюс (работа положительна), а фигуры под осью – со знаком минус (работа отрицательна).

Мощность.

Для характеристики скорости, с которой совершается работа, вводят величину, называемую мощностью Р. Мощность это работа, совершаемая силой за единицу времени. Если за время dt сила совершает работу 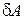, то мощность, развиваемая этой силой в данный момент времени

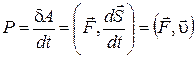. (1.6.3)

Таким образом, мощность, развиваемая силой, равна скалярному произведению силы на скорость, с которой движется точка приложения силы.

Зная мощность, можно найти работу, совершаемую силой за промежуток времени t 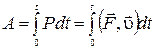. (1.6.4)

Единицей работы в системе СИ является Джоуль (Дж), а единицей мощности – Ватт (Вт).

Кинетическая энергия.

Имея в виду, что 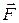=md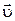/dt и d= 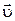dt, запишем

δА =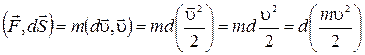. (1.6.5)

Отсюда видно, что работа результирующей силы 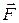идет на приращение некоторой величины (стоящей в скобках), которую называют кинетической энергией (энергией движения):

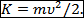(1.6.6)

Таким образом, приращение кинетической энергии частицы при элементарном перемещении равно элементарной работе всех сил, действующих на частицу

dK = δА, (1.6.7)

а при конечном перемещении из точки 1 в точку 2

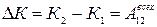(1.6.8)

т. е. приращение кинетической энергии частицы, на некото­ром перемещении равно алгебраической сумме работ всех сил, действующих на частицу на том же перемещении. Если А₁₂ > 0, то К₂ >К₁, т. е. кинетическая энергия частицы увели­чивается; если А₁₂ < 0, то кинетическая энергия уменьшается.

Соотношение (1.6.8) называют часто теоремой об изменении кинетической энергии.

Дата добавления: 2014-01-06