Три формы записи интеграла

==

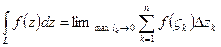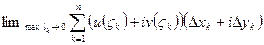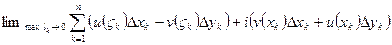== . Это – 1 форма записи – в виде двух криволинейных интегралов.

Параметризуем дугу L: , .

. Подставляя в первую форму записи, имеем:

= .

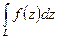Это – 2 ая форма записи – в виде двух определенных интегралов.

Параметризуем дугу L:z=z(t),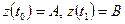

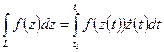. Это – третья форма записи – в виде определенного интеграла от комплексно - значной фунции действительной переменной.

Пример. Вычислить 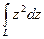по трем различным дугам: 1) OB: y=x, 2) OB: y=x^2, 3) OAB   1) Воспользуемся третьей формой записи интеграла, параметризуя дугу OB: (1+i)t, O(0,0) (t=0), B(1,i) (t=1). z^2 = (1+i)^2 t^2, dz = (1+i) dt. = = =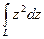

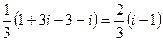
2) .

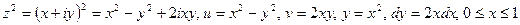По первой форме записи интеграла

=

=.

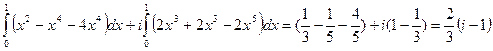3) OA: y = 0, dy = 0. AB: x =1, dx = 0. Поэтому

.

Как оказалось, результат во всех трех случаях один и тот же. В чем же здесь дело? Это – случай или закономерность? Ответ на этот вопрос дает интегральная теорема Коши.

Интегральная теорема Коши (для односвязной области).

Пусть G – односвязная область, пусть функция f(z) – аналитическая в G функция, пусть L – кусочно—гладкий контур, принадлежащий области G. Тогда .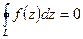

Теорему можно сформулировать и так: интеграл от аналитической функции вдоль кусочно-гладкого контура равен нулю.

Доказательство.

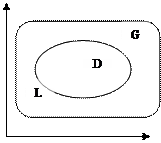
Обозначим D – внутренность контура L. Запишем формулу Грина 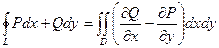. Представим интеграл в первой форме записи через два криволинейных интеграла =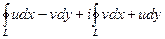

Применим к каждому слагаемому в правой части равенства формулу Грина. В первом интеграле примем P = u, Q = -v.

(для аналитической функции выполнены условия Коши – Римана ).

Во втором интеграле примем P = v, Q = u.

(условие Коши – Римана).

Поэтому .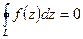

Следствие. Пусть L₁, L₂ – две кусочно-гладких дуги в односвязной области G, соединяющие точки A, B. Пусть функция f(z) – аналитическая в области G. Тогда = .

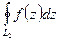Можно дать словесную формулировку: интеграл от аналитической функции в односвязной области вдоль кусочно-гладкой дуги не зависит от формы дуги, а зависит только от начальной и конечной точек дуги.

Доказательство. Образуем контур 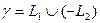. По интегральной теореме Коши

. Но . Следовательно, .= .

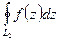Поэтому результат в рассмотренном выше примере не случаен.

Очень важный пример. Вычислить интеграл 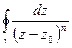, где n – целое число, контур 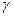- окружность с центром в точке радиусом .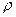

Покажем, что точки z на контуре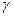можно описать уравнением 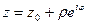, , 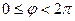- действительное число. В самом деле, , так как . Таким образом, контур 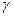- это геометрическое место точек комплексной плоскости, расположенных на расстоянии 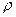от точки - окружность с центром в точке радиусом .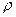

Если , то подынтегральная функция – аналитическая внутри контура 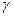. Тогда по интегральной теореме Коши 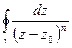= 0.

Пусть 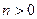. Так как точка z лежит на контуре 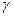, то 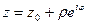, . Перейдем к переменной 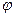. Пусть .

=

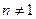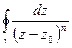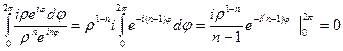
по периодичности экспоненты.

Пусть 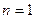. Тогда

=.

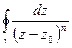Вывод. =.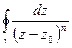

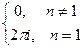Дата добавления: 2014-01-06