
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функциональные ряды
|
|
|
|
Функциональный ряд 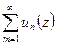 в каждой фиксированной точке
в каждой фиксированной точке  представляет собой числовой ряд. Исследуя этот числовой ряд, можно выяснить, сходится или расходится функциональный ряд в данной точке z.
представляет собой числовой ряд. Исследуя этот числовой ряд, можно выяснить, сходится или расходится функциональный ряд в данной точке z.
Функциональный ряд 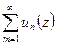 сходится в точке
сходится в точке  , если
, если 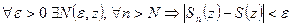 . Это так называемая обычная или поточечная сходимость функционального ряда, заметим, что
. Это так называемая обычная или поточечная сходимость функционального ряда, заметим, что  зависит не только от
зависит не только от 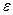 , как в числовых рядах, но и от z, поэтому ряд может сходиться с разной скоростью в различных точках z.
, как в числовых рядах, но и от z, поэтому ряд может сходиться с разной скоростью в различных точках z.
Критерий Коши ( поточечной сходимости ряда).Для того чтобы функциональный ряд 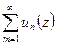 сходился в точке z, необходимо и достаточно, чтобы
сходился в точке z, необходимо и достаточно, чтобы  .
.
Множество точек z, в которых функциональный ряд сходится, называется областью сходимости функционального ряда.
Примеры
1. Ряд  сходится на всей комплексной плоскости. Проверим это. Исследуем ряд из модулей
сходится на всей комплексной плоскости. Проверим это. Исследуем ряд из модулей  . Так как это числовой знакоположительный ряд, применим к нему признак Даламбера.
. Так как это числовой знакоположительный ряд, применим к нему признак Даламбера. 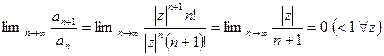 . Ряд абсолютно сходится во всей комплексной плоскости.
. Ряд абсолютно сходится во всей комплексной плоскости.
2. Ряд 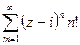 сходится только в точке
сходится только в точке  . Проверьте это.
. Проверьте это.
3. Ряд 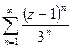 абсолютно сходится в круге
абсолютно сходится в круге  , проверьте это по признаку Даламбера или радикальному признаку Коши. На окружности
, проверьте это по признаку Даламбера или радикальному признаку Коши. На окружности 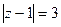 ряд
ряд 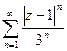 превращается в ряд из единиц, расходящийся, так как не выполняется необходимый признак сходимости ряда.
превращается в ряд из единиц, расходящийся, так как не выполняется необходимый признак сходимости ряда.
4. Ряд 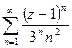 абсолютно сходится в круге
абсолютно сходится в круге  , проверьте это по признаку Даламбера или радикальному признаку Коши. На окружности
, проверьте это по признаку Даламбера или радикальному признаку Коши. На окружности 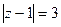 ряд
ряд  превращается в сходящийся ряд
превращается в сходящийся ряд  .
.
5. Ряд  абсолютно сходится в круге
абсолютно сходится в круге  , проверьте это по признаку Даламбера или радикальному признаку Коши. Исследуем сходимость на окружности
, проверьте это по признаку Даламбера или радикальному признаку Коши. Исследуем сходимость на окружности 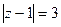 в различных ее точках. В точке
в различных ее точках. В точке 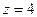 имеем расходящийся гармонический ряд. В точке
имеем расходящийся гармонический ряд. В точке 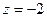 имеем ряд
имеем ряд 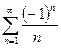 . Это – условно сходящийся ряд (по признаку Лейбница). В точке
. Это – условно сходящийся ряд (по признаку Лейбница). В точке 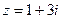 имеем ряд
имеем ряд 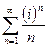 . Этот ряд рассмотрен выше, он сходится условно. В точке
. Этот ряд рассмотрен выше, он сходится условно. В точке 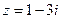 имеем ряд
имеем ряд  . Он тоже сходится условно, так как условно сходятся ряды из действительных и мнимых частей.
. Он тоже сходится условно, так как условно сходятся ряды из действительных и мнимых частей.
Функциональный ряд 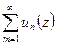 сходится равномерно в области G если
сходится равномерно в области G если 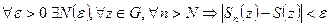 . Это – равномерная сходимость функционального ряда в области G, заметим, что
. Это – равномерная сходимость функционального ряда в области G, заметим, что  зависит только от
зависит только от 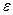 , как в числовых рядах, поэтому ряд сходится с одной и той же скоростью в различных точках z области G.
, как в числовых рядах, поэтому ряд сходится с одной и той же скоростью в различных точках z области G.
Критерий Коши ( равномерной сходимости ряда).Для того чтобы функциональный ряд 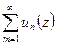 сходился равномерно в области G, необходимо и достаточно, чтобы
сходился равномерно в области G, необходимо и достаточно, чтобы 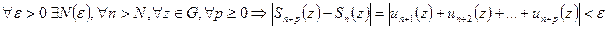 .
.
Для равномерно сходящихся функциональных рядов функций комплексной переменной справедливы теоремы о непрерывности суммы ряда, о почленном интегрировании и почленном дифференцировании. Формулировки этих теорем и доказательства идентичны теоремам о равномерно сходящихся рядах функций действительного переменного. Разница лишь в различном понимании модуля действительного и комплексного числа и в том, что интегрирование проводится по кусочно-гладкой дуге..
Аналогично формулируется и доказывается и признак Вейерштрасса равномерной сходимости ряда.
Признак Вейерштрасса. Пусть члены функционального ряда 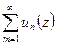 мажорируются членами сходящегося числового ряда в некоторой области
мажорируются членами сходящегося числового ряда в некоторой области 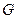
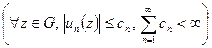 . Тогда функциональный ряд сходится равномерно в области G.
. Тогда функциональный ряд сходится равномерно в области G.
Доказательство. Для сходящегося числового знакоположительного ряда  выполнен критерий Коши:
выполнен критерий Коши: 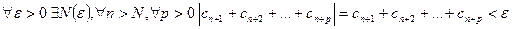 .
.
Так как 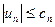 (по свойствам сходящихся числовых рядов можно считать, что неравенство выполняется, начиная с первого номера, т.е. для всех n), поэтому для функционального ряда выполнен критерий Коши равномерной сходимости ряда:
(по свойствам сходящихся числовых рядов можно считать, что неравенство выполняется, начиная с первого номера, т.е. для всех n), поэтому для функционального ряда выполнен критерий Коши равномерной сходимости ряда:
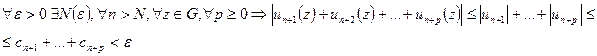 Следовательно, функциональный ряд сходится равномерно в области G.
Следовательно, функциональный ряд сходится равномерно в области G.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 363; Нарушение авторских прав?; Мы поможем в написании вашей работы!