ВВЕДЕНИЕ. Утверждено в качестве учебного пособия

Воротников С.М.

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ ЛОГИКУ

С.М. Воротников

Утверждено в качестве учебного пособия

Ученым советом Государственного образовательного учреждения

высшего профессионального образования

«Комсомольский-на-Амуре государственный технический университет»

Комсомольск-на-Амуре 2003

УДК 517.11 (07)

ББК 22.122 я7

В 75

В 75 Введению в математическую логику.: Учебно-практ. пособие. – Комсомольск-на-Амуре: Государственное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре гос. техн. ун-т», 2003. – 61 с.

По содержанию данное пособие тесно связано с конспектом лекций [1] и является методической основой для самостоятельного изучения следующих вводных разделов математической логики и ее приложений: формулы логики высказываний и операции над ними; упрощение записи формул; доказательство равносильности, тождественной истинности и тождественной ложности формул; приведение формул логики высказываний к нормальным формам; использование формул логики высказываний в теории конечных автоматов; формулы логики предикатов и операции над ними; исследование выполнимости, истинности, ложности и равносильности формул логики предикатов, приведение формул логики предикатов к предваренной (пренексной) нормальной форме; основы исчисления высказываний и исчисления предикатов.

Рассмотрены примеры решения задач по указанным темам, приведены задачи и упражнения для самостоятельного решения, контрольные вопросы по теории и варианты индивидуальных заданий.

Для студентов электротехнических специальностей, обучающихся по дистанционной технологии.

ББК 22.122 я7

© Государственное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет», 2003

© Институт новых информационных технологий Государственного образовательного учреждения высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет», 2003

Разделы, связанные с математической логикой, входят в обязательный федеральный стандарт по ряду направлений и специальностей подготовки специалистов с высшим образованием. Между тем, учебной литературы, ориентированной на будущих технических специалистов, практически нет.

Данное пособие в основном основывается на материале конспекта лекций [1], но может использоваться и независимо от других источников.

Каждой теме предпослано краткое введение, содержащее определения основных понятий и теоретических результатов, используемых в соответствующих задачах. Приводятся примеры решения типовых задач, упражнения для самостоятельной работы, контрольные вопросы по теории и варианты индивидуального домашнего задания (контрольной работы).

Пособие охватывает следующую тематику: формулы логики высказываний и операции над ними; упрощение записи формул; доказательство равносильности, тождественной истинности и тождественной ложности формул; приведение формул логики высказываний к нормальным формам; использование формул логики высказываний в теории конечных автоматов; формулы логики предикатов и операции над ними; исследование выполнимости, истинности, ложности и равносильности формул логики предикатов, приведение формул логики предикатов к предваренной (пренексной) нормальной форме; основы исчисления высказываний и исчисления предикатов.

Использованы следующие общепринятые обозначения:

N, Z, Q, R, C, – множества натуральных, целых, рациональных, действительных, комплексных чисел соответственно;

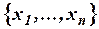– множество, состоящее из элементов ;

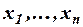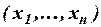– упорядоченный набор из 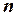элементов (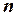-мерный вектор, 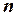-ка);

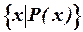– множество таких элементов 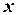, для которых выполняется условие (свойство) .

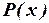Дата добавления: 2014-01-06