
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сводка теории. Высказывания и операции над ними, формулы
|
|
|
|
Высказывания и операции над ними, формулы
ЭЛЕМЕНТЫ ЛОГИКИ ВЫСКАЗЫВАНИЙ
Имена предметов называются индивидными (предметными) константами. В «грамматике» формального языка индивидные константы играют роль существительных.
Выражения, содержащие знаки «переменных» и превращающиеся в имена предметов, если вместо переменных подставить некоторые имена предметов, называются именными формами. Именные формы мы будем называть индивидными (предметными) переменными. Областью изменения индивидных переменных являются не только числа, но и совокупность любых индивидов (в частности, для нематематического языка – любые предметы или даже любые утверждения). В «грамматике» формального языка индивидные переменные играют роль местоимений.
Соединяя два имени чисел знаками равенства или неравенства, получаем записи некоторых утверждений – это высказывания, называемые еще пропозициональными переменными, если они содержат индивидные переменные.
Общее логико-философское определение этого понятия можно сформулировать так: высказывание – это мысленное отражение объективной связи между предметами. Оно истинно, если адекватно отражает эту связь, в противном случае – ложно. В естественном языке высказывание существует в виде повествовательного предложения. Если это предложение простое, т.е. описывает отдельный факт и не может быть разделено на более мелкие осмысленные предложения, то соответствующее высказывание называется простым.
В формальном языке высказывание представляется выражением, содержащим индивидные константы и некоторые специальные символы, обозначающие связь между ними. В математической логике высказывания рассматриваются лишь с позиции их свойства быть истинными или быть ложными, конкретное содержание высказываний игнорируется.
Роль союзов, с помощью которых в естественном языке из простых предложений формируются сложные, в формальном языке играют логические (или пропозициональные) связки, называемые также логическими операциями.
Будем интерпретировать логические связки как функции, определенные на так называемом булевом (по имени английского математика Дж. Буля) множестве В = { И, Л }, {«истина», «ложь»} или { 1, 0 }, со значениями в этом же множестве следующим образом:
| отрицание | 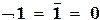 , , 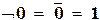 ; ;
|
| конъюнкция | 1&1 =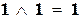 , , 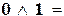 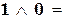 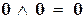 ; ;
|
| дизъюнкция | 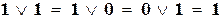 , , 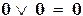 ; ;
|
| импликация | 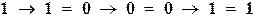 , , 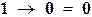 ; ;
|
| эквивалентность | 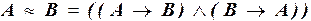 . .
|
Действие этих операций (связок) можно представить в виде символических таблиц, которые будем называть таблицами истинности данных логических операций. Например, для операции отрицания таблица истинности выглядит так:
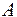
| 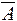
|
Именно эту таблицу (ее надо читать по строкам: «если 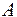 =1, то
=1, то 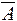 = = 0», т.е. одновременно
= = 0», т.е. одновременно 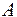 истинно и
истинно и 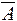 ложно) мы фактически и приняли в качестве определения операции отрицания.
ложно) мы фактически и приняли в качестве определения операции отрицания.
В технических приложениях операцию отрицания называют инверсией. Эту операцию можно условно проиллюстрировать работой следующей электрической цепи (рис. 1.1).
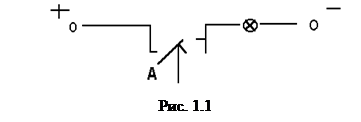
Действие в цепи: если 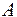 = 1, то кнопка нажата, цепь разомкнута и лампочка не горит, т.е.
= 1, то кнопка нажата, цепь разомкнута и лампочка не горит, т.е. 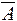 = 0; если
= 0; если 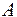 = 0, то цепь замкнута и лампочка горит, т.е.
= 0, то цепь замкнута и лампочка горит, т.е. 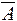 = 1.
= 1.
Таблица истинности для операции конъюнкции, соответствующей союзу «и» естественного языка, выглядит следующим образом:
| A | В | A^B |

В этой таблице каждая строка показывает, истинна или ложна конъюнкция при данном наборе истинных или ложных конъюнктивных членов. В технических приложениях операция конъюнкции называется логическим умножением. Эту операцию можно проиллюстрировать работой следующей электрической цепи (рис. 1.2).
Таблица истинности для операции дизъюнкции (аналог в естественном языке – союз «или») выглядит следующим образом:
| А | В | AÚB |

В технических приложениях операцию дизъюнкции называют логическим сложением. Простейшая электрическая цепь, иллюстрирующая эту операцию, имеет вид (рис. 1.3).
В отдельных технических дисциплинах (а иногда и в математических теориях) используют и исключающее «или», приводящее к операции «альтернативная дизъюнкция», которую обозначают «+2» (а также «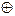 », «
», «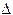 »). Примером такой операции в математике является сложение по модулю 2. Результаты операций A Ú B и A
»). Примером такой операции в математике является сложение по модулю 2. Результаты операций A Ú B и A 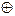 B отличны лишь в одной ситуации: когда A = 1 и B = 1 одновременно.
B отличны лишь в одной ситуации: когда A = 1 и B = 1 одновременно.
Таблица истинности для операции альтернативной дизъюнкции выглядит следующим образом:
| А | В | A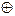 B B
|
Эту операцию можно проиллюстрировать работой следующей электрической цепи (рис.1.4).
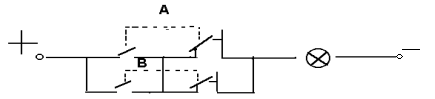
Таблица истинности для операции импликации (ближайший аналог в естественном языке – оборот «если..., то...») такова:
| A | В | A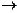 B B
|
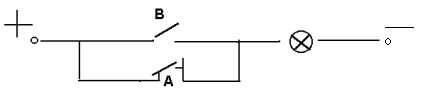
Соответствующая электрическая цепь имеет вид (рис. 1.5).
Приведем таблицу истинности для эквивалентности (соответствует оборотам естественного языка типа «тогда и только тогда, когда...», «для того, чтобы..., необходимо и достаточно...» и др.):
| A | В | A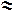 B B
|
Электрическая цепь, реализующая операцию эквивалентности, имеет вид (рис. 1.6)

Понятие формулы алгебры логики (высказываний) определим следующим образом:
1) пропозициональная переменная есть формула;
2) если А и В – формулы, то
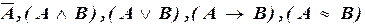 – формулы;
– формулы;
3) других формул, кроме построенных по пп. 1, 2, нет.
Подформулой формулы А называется любая ее часть, которая сама является формулой.
Каждая формула может интерпретироваться как функция, определенная на множестве В, со значениями в этом же множестве, полученная из 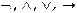 по правилам построения данной формулы. Значением формулы А при данных значениях переменных во множестве В называется значение функции, соответствующей формуле А, при этих значениях переменных.
по правилам построения данной формулы. Значением формулы А при данных значениях переменных во множестве В называется значение функции, соответствующей формуле А, при этих значениях переменных.
Формула называется выполнимой (опровержимой), если существует такой набор значений переменных, при которых эта формула принимает значение 1 (0).
Формула называется тождественно-истинной, или тавтологией (тождественно-ложной, или противоречием), если эта формула принимает значение 1 (0) при всех наборах значений переменных.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 317; Нарушение авторских прав?; Мы поможем в написании вашей работы!