Применение формул логики высказываний в теории однотактных дискретных автоматов

Задачи

.

2). Для получения СКНФ преобразуем каждый конъюнктивный член:

;

.

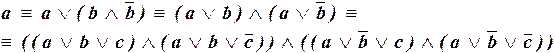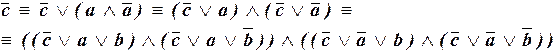Тогда имеем:

.

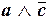
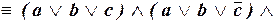
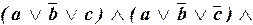
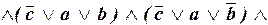
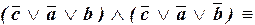
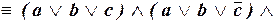
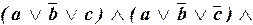
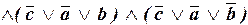Пример 1.16

Преобразовать формулы к ДНФ:

а) ;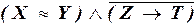

б) ;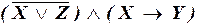

в) ;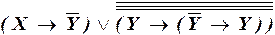

г) .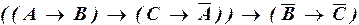

Решение

а)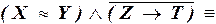

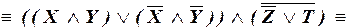
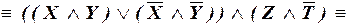
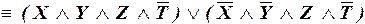– СДНФ.

б)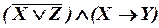

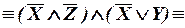
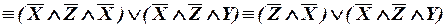
- ДНФ.

в)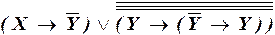

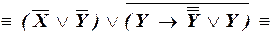
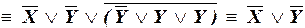– ДНФ.

г)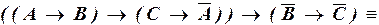

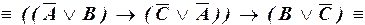
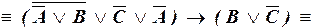
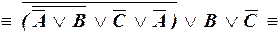
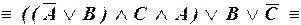
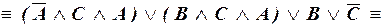
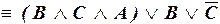– ДНФ.

Пример 1.17

Построить цепь для электрифицированной игры с монетами. По установленному сигналу каждый из двух игроков замыкает или размыкает переключатель, находящийся под его управлением. Если оба игрока делают одно и то же, то выигрывает первый игрок (А); если противоположное, то выигрывает второй игрок (В). Построить цепь так, чтобы загоралась лампочка, если выигрывает игрок А. Записать ДНФ соответствующей формулы.

Решение

Обозначим переменными А и В действия игроков, приписывая переменной значение 1, если игрок замыкает свой переключатель, и 0, если размыкает. Тогда таблица истинности для искомой формулы будет иметь следующий вид:

По описанной ранее технологии с помощью строк, в которых формула принимает значение 1, записываем ДНФ:

.

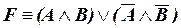Для построения соответствующей электрической цепи будем использовать прямые (для описания значений А и В) и обратные (для описания значени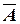й и 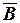) двухпозиционные переключатели. Значение 1 переменной интерпретируется как состояние переключателя «ток проходит», значение 0 – «ток не проходит». Последовательное соединение переключателей будет имитировать конъюнкцию соответствующих переменных (ток по этому участку цепи пойдет только в случае, когда обе переменные истинны одновременно). Параллельное соединение будет имитировать

дизъюнкцию.

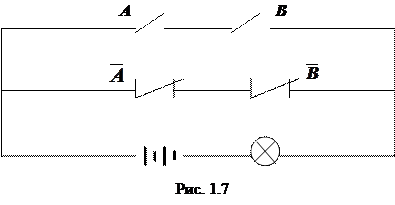
Тогда условиям задачи будет удовлетворять, например, следующая электрическая цепь (рис. 1.7).

1.16. Привести к ДНФ:

а) ;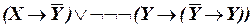

б) .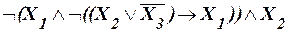

1.17. Привести к СДНФ формулы из задачи 1.16.

1.18. Доказать тождественную истинность формул:

а) ;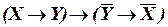

б) ;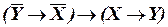

в) ;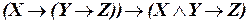

г) ;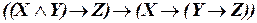

д) .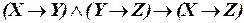

1.19. Доказать тождественную ложность формул:

а) ;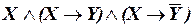

б) .

1.20. Привести формулы к ДНФ (с помощью тождественных преобразований) и, если можно, упростить:

а) ;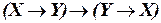

б) ;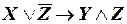

в) ;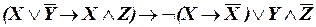

г) ;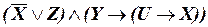

д) ;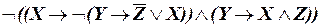

е) ;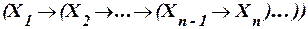

ж) .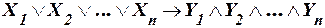

1.21. Доказать тождественную истинность формул:

а) ;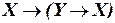

б) ;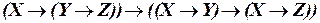

в) ;

г) .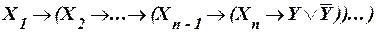

1.22. Доказать тождественную ложность формул:

а) ;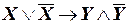

б) ;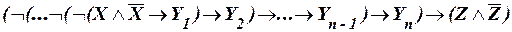

в) .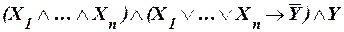

1.23. Двумя способами: с помощью истинностных таблиц и с помощью тождественных преобразований привести к СДНФ формулы из задачи 1.20.

1.24. Привести к СДНФ, т.е. найти СДНФ, равносильную данной формуле:

а) ;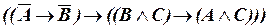

б) ;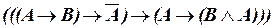

в) .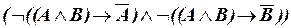

1.25. Привести к СКНФ, т.е. найти СКНФ, равносильную данной формуле:

а) ;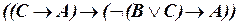

б) ;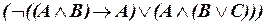

в) .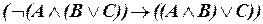

1.26. Пусть формула U записана в СКНФ. Строим формулу В следующим образом:

1) выписываем конъюнкцию дизъюнктивных членов, не входящих в U;

2) меняем Ù на Ú, Ú на Ù, 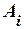на , на .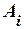

Доказать, что В – СДНФ формулы U.

1.27. По СКНФ формулы U построить:

а) СКНФ формулы ;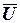

б) СДНФ формулы .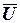

1.28. По СДНФ формулы U и СДНФ формулы В построить:

а) СКНФ и СДНФ формулы ;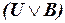

б) СКНФ и СДНФ формулы ;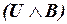

в) СКНФ и СДНФ формулы .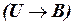

Дата добавления: 2014-01-06