Пример 1.13

Примеры

Убедиться, является ли данная формула ДНФ, КНФ, СДНФ или СКНФ:

а) ;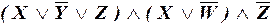

б) ;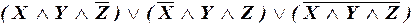

в) ;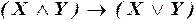

г) ;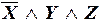

д) ;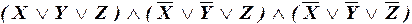

е) .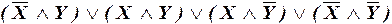

Решение

а) Данная формула является КНФ (конъюнкция элементарных дизъюнкций), но не СКНФ, так как элементарные дизъюнкции не являются полными.

б) Формула не является ДНФ, так как последняя конъюнкция не является элементарной. Но формулу можно с помощью закона Де Моргана преобразовать к равносильному виду

,

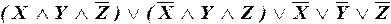который является ДНФ, но не СДНФ (не все элементарные конъюнкции полны).

в) Формула не является ни ДНФ, ни КНФ, поскольку содержит импликацию.

г) СДНФ, состоящая из одной элементарной полной конъюнкции; либо КНФ, но не СКНФ, так как состоит из трех элементарных неполных дизъюнкций.

д) СКНФ.

е) СДНФ.

Пример 1.14

Зная таблицу истинности формулы F, записать ее СДНФ и СКНФ:

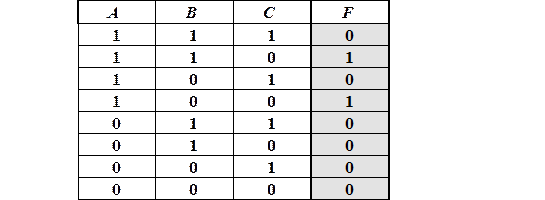
Решение

1) Получение СДНФ.

Выбираем те наборы значений А, В, С, при которых F = 1, и строим по ним соответствующие элементарные конъюнкции:

1 1 0 ,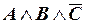

1 0 0 .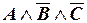

Тогда дизъюнкция этих элементарных конъюнкций и будет СДНФ формулы F:

.

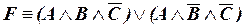2) Получение СКНФ.

Выбираем те наборы значений А, В, С, при которых F = 0, и строим по ним соответствующие элементарные дизъюнкции:

1 1 1 ,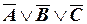

1 0 1 ,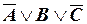

0 1 1 ,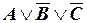

0 1 0 ,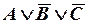

0 0 1 ,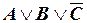

0 0 0 .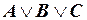

Тогда конъюнкция этих элементарных дизъюнкций и будет СКНФ формулы F:

.

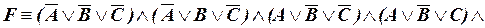
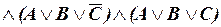Пример 1.15

Преобразовать формулу F(a, b. c)= 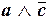к СДНФ и СКНФ.

Решение

1). Получим вначале СДНФ:

Дата добавления: 2014-01-06