
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры. Записать фразы в виде формул логики предикатов, указав области определения используемых предикатов:
|
|
|
|
Пример 2.1
Записать фразы в виде формул логики предикатов, указав области определения используемых предикатов:
а) если х делится на у и у делится на z, то х делится на z;
б) х – простое число.
Решение
а) Разбивая фразу на простые предложения, видим, что используется только одно свойство двух объектов, поэтому введем предикат 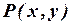 = «
= «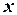 делится на
делится на  «. Речь идет, очевидно, о делимости нацело, поэтому областью определения предиката будет множество целых чисел:
«. Речь идет, очевидно, о делимости нацело, поэтому областью определения предиката будет множество целых чисел: 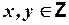 .
.
Структура всей фразы описывается конструкцией «если..., то...», значит, самой внешней (последней) связкой нашей формулы будет импликация. Посылка этой импликации описывается конъюнкцией простых предложений, поэтому итоговая формула имеет вид:
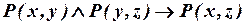 .
.
б) Самый простой подход: ввести предикат 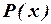 = «
= «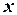 – простое число», который и описывает всю фразу.
– простое число», который и описывает всю фразу.
Но математические термины должны быть определены однозначно (что такое «простое» число, которое записывается одной цифрой? или которое записано с помощью повторения одной цифры? или которое можно легко запомнить или записать?), поэтому точный смысл этой фразы может быть воспроизведен с помощью строгого определения. То есть «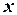 делится только на 1 и на себя» или, еще точнее, «либо
делится только на 1 и на себя» или, еще точнее, «либо 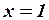 , либо
, либо 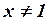 и если
и если 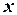 делится на любое
делится на любое 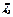 , то, или
, то, или  , или
, или 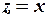 «.
«.
В последней фразе использован предикат делимости 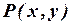 (см. пункт а), предикат равенства
(см. пункт а), предикат равенства 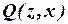 = «
= «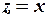 «и квантор всеобщности. Поскольку понятие простого числа обычно вводят только для натуральных чисел, то
«и квантор всеобщности. Поскольку понятие простого числа обычно вводят только для натуральных чисел, то  . Формула, описывающая последнюю фразу, имеет вид:
. Формула, описывающая последнюю фразу, имеет вид:
 .
.
Пример 2.2
Указать свободные и связанные вхождения переменных в формулы:
а) 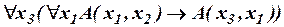 ;
;
б)  ;
;
в) 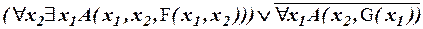 .
.
Решение
Проанализируем область действия каждого квантора, отмечая связанные вхождения общей прямой с засечками снизу, а свободные вхождения переменных стрелочкой сверху. Отметим, что в третьей формуле F и G – функциональные символы (в теориях первого порядка аргументом предиката не может выступать другой предикат).
¯ ¯




 а)
а) 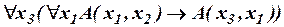 ;
;
¯ ¯



 б)
б)  ;
;
¯










 в)
в) 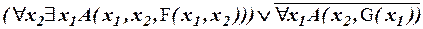 .
.
 |
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1525; Нарушение авторских прав?; Мы поможем в написании вашей работы!