Непрерывность функции. Разрывнве функции

Пример.

Предел .

Пусть в некотором множестве определена функция , .

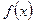Определение (по Гейне). Функция 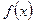называется непрерывной в точке 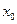, если для любой последовательности значение аргумента сходящейся к 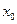последовательность соответствующих значений функций, т.е. 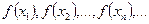сходится к .

Другими словами функция непрерывна в точке 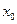, если существует предел и он равен значению функции в этой точке, т.е. 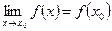(1)

Так как , то соотношению (1) можно придать следующую форму , т.е. для непрерывной функции знак функции и предела можно переставлять.

Определение (по Коши). Функция 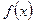называется непрерывной в точке 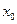, если для любого 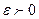существует , такое, что для , удовлетворяющих неравенству выполняется неравенство .

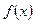Замечание. Если или слева, то функцию называют непрерывной в точке 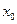справа или слева. Если функция непрерывна и справа, и слева, то она непрерывна в этой точке.

Теорема. Если функци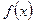и и 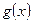непрерывны в точке 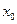, то функции , и , при 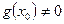, также являются непрерывными в этой точке.

Простейшим примером непрерывной функции являются элементарные функции.

Определение. Точка 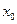называется точкой разрыва функции 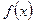, если 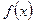в точке 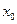не является непрерывной.

Разрывы функции можно классифицировать следующим образом:

1. Разрыв первого рода, точка 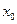называется точкой разрыва первого рода, если в этой точке функция 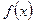имеет конечные, но не равные друг другу левый и правый пределы, т.е. .

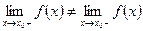2. Разрыв второго рода, точка 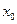называется точкой разрыва второго рода, если в этой точке функция 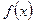не имеет по крайней мере одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.

Пример: исследовать на непрерывность функцию ,

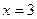
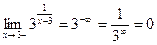
Определение. Функция 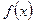называется кусочно-непрерывной на отрезке 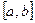, если она непрерывна во всех внутренних точках отрезка 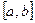, за исключением конечного числа точек, которые имеют разрыв первого рода и кроме того имеет односторонние пределы в точках и .

Определение. Функция 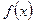называется кусочно-непрерывной на интервале, если она кусочно-непрерывна на любом принадлежащем ему отрезке.

Дата добавления: 2014-01-06