Численный пример

Рассмотрим функцию Z(x)= tg(x) – x + 2. Как было установлено, промежуток локализации корня для этой функции от -2 до -1.5, а=-2, b=-1.5 Требуется вычислить корень функции с точностью ε = 0.0001 Сначала необходимо найти первую и вторую производные

В качестве начального приближения x₀ выберем значение -1.5 (x₀=-1.5), так как знаки функции и ее второй производной совпадают (Z(-1.5) = -10.6 Z’’(-1.5)= -0.0005).

Сначала найдем корень функции без использования компьютера. Чтобы ограничить количество итераций определим с точность ε=0.05.

Шаг 1. Вычислим х₁.

Z(x₀)= -10.6014, первая производная z’(x₀) = 198.86

│x₁ – x₀ │= 0.054. Поскольку требуемая точность не достигнута, продолжаем вычисления.

Шаг 2.

Z(x₁)=-4.569, Z’(x₁) = 64.256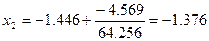

│x₂ – x₁ │= 0.07 > 0.05

Шаг 3

Z(x₂)=-1.681, Z’(x₂)= 25.575

│x₃ – x₂ │= 0.067 >0.05

IШаг 4.

Z(x₃)=-0.435, Z’(x₃)=14.02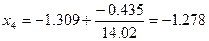

│x₄ – x₃ │=0.021 <0.05, поэтому считаем, что корень найден и равен -1.2878, Z(-1.287)=0.04

Для вычислений на компьютере выберем точность 0.0001

В таблице 4 представлены вычисления на рабочем листе MS Excel

В колонке А указывается номер итерации i, в колонке В – значение x_i, в колонках C и D рассчитываются значения функции Z(x_i)и ее производной Z’(x_i)

Разность между х₆ и х₅ (│х₆ - х₅│= 0.00007) по абсолютному значению меньше заданной точности ε = 0.0001, поэтому считаем, что корень Z(x) = -1.274.

Таблица 4

A	B	C	D
	i	Xi	Z(Xi)	Z'(Xi)
		-1.5	-10.60142	198.85004
		-1.44669	-4.56927	64.25558
		-1.37558	-1.68159	25.57491
		-1.30982	-0.43461	14.02079
		-1.27883	-0.04830	11.06979
		-1.27446	-0.00075	10.72704
		-1.27439	0.00000	10.72165
	Корень

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 1

1. С точностью до 0,0005 вычислить все корни уравнения:

а) ,

б)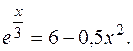

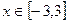
2. Для N=20 вычислить интеграл

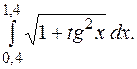
Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 2

2. С точностью до 0,0005 вычислить все корни уравнения:

а) ,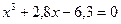

б)

3. Приняв N=20, вычислить интеграл

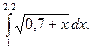
Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 3

1. С точностью до 0,0005 вычислить все корни уравнения:

а) ,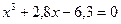

б)

2. Приняв N=20, вычислить интеграл

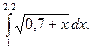
Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 5

1. С точностью до 0,0005 вычислить все корни уравнения:

а) ,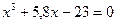

б)

2. Приняв N=20, вычислить интеграл

Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 6

1. С точностью до 0,0005 вычислить все корни уравнения:

а) ,

б)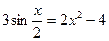

2. Приняв N=20, вычислить интеграл

Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 7

1. С точностью до 0,0005 вычислить все корни:

а) ,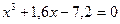

б)

2. Приняв N=20, вычислить интеграл

Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 8

1. С точностью до 0,0005 вычислить все корни уравнений:

а) ,

б)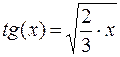

2. Приняв N=20, вычислить интеграл

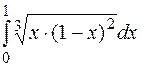
Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 9

1. С точностью до 0,0005 вычислить все корни уравнения:

а) ,

б)

2. Приняв N=20, вычислить интеграл

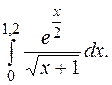
Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 10

1. С точностью до 0,0005 вычислить все корни уравнения:

а) ,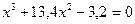

б)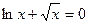

2. Приняв N=20, вычислить интеграл

Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 4

1. С точностью до 0,0005 вычислить все корни уравнения:

а) ,

б)

2. Приняв N=20, вычислить интеграл

Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Индивидуальное задание

по разделу "Численные методы”(часть 2).

Вариант 11

1. С точностью до 0,0005 вычислить все корни уравнений:

а) ,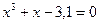

б)

2. Вычислить интеграл при N=20

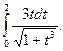
Оценить погрешность результата по правилу Рунге (методом двойного счёта).

Дата добавления: 2014-01-06