Дифракция Фраунгофера

Дифракция от круглого диска

Если диск закрытых m зон Френеля (рассчитывается по формуле (4.5)), то

,

откуда 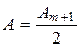. При m малом .

Пусть на бесконечно длинную щель падает плоская волна. За щелью поместим линзу и экран так, что экран лежит в фокальной плоскости линзы. Так как щель бесконечна, достаточно рассмотреть дифракцию в одной плоскости, перпендикулярной щели.

Разобьем волновую поверхность в щели на зоны шириной 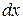, которые параллельны краям щели. Вторичные волны, посылаемые зонами в направлении, определяемом углом j, соберутся в точке Р экрана. Так как линза собирает в фокальной плоскости плоские волны, то в (4.0) отсутствует. Ограничимся рассмотрением малых углов j, тогда коэффициент К будем считать постоянным. Тогда согласно принципу Гюгенса-Френеля каждая зона создает в точке Р колебания с амплитудой

(4.6)

, зависящей только от площади зоны

Обозначим через А₀ алгебраическую сумму амплитуд, возбуждаемую в точке Р всеми зонами.

Ее можно найти, проинтегрировав по всей щели в

,

откуда (4.6) Сопоставим фазы возбуждаемых колебаний в точке Р зонами с координатами О и Х. Оптические пути ОР и QP таухотронны. Следовательно, разность фаз образуется на пути . Если начальную фазу колебаний в точке О принять равной 0, то начальная фаза колебаний, возбуждаемых зоной с координатой х, будет равна

(4.8)

Тогда, подставив (4.7), (4.8) в (4.6), получим колебания, создаваемые зоной с координатой Х

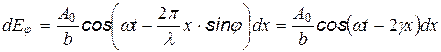
где .

Проинтегрировав выражение по ширине зоны, найдем результирующее колебание в точке Р, создаваемое волновой поверхностью в пределах щели:

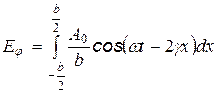
Интегрирование дает

При

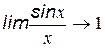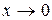1- замечательный предел (при )

при

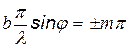
- количество минимумов

Таким образом, поле интегрирования получаем:

,

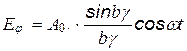где (4.10)

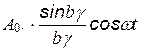- есть амплитуда колебаний .

при (то есть точка Р напротив щели)

- первый замечательный предел и результирующая амплитуда равна .

Минимальная амплитуда 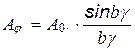будет при (m =1,2,3…) – условие минимумов интенсивности.

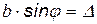- оптическая разность хода лучей от краев щели.

Учитывая, что интенсивность из 4.10 получим для интенсивности в точке Р

(4.12)

Из 4.12, так как иследует , то есть картина симметрична относительно центра линзы.

Если изобразить график интенсивности

Из (4.11) можно найти количество минимумов интенсивности (т.к.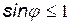

То есть когда ширина щели минимумов вообще не возникает.

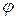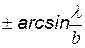Краям центрального максимума соответствуют углы следующие из условия : эти значения равны , откуда угловая ширина центрального максимума при .

Дата добавления: 2014-01-06