Радиоактивность. Определение. Явление радиоактивности представляет собой процесс самопроизвольных ядерных превращений с испусканием излучений

Определение. Явление радиоактивности представляет собой процесс самопроизвольных ядерных превращений с испусканием излучений. Все самопроизвольные превращения имеют общую закономерность: характер поведения во времени больших количеств неустойчивых или возбужденных частиц, а следовательно, и их продуктов распада одинаков для любого типа распада, так как все распады протекают по вероятностным законам. Константы соответствующих временных распределений также имеют один и тот же физический смысл независимо от природы распада.

Закон распада. Основное предположение, из которого вытекает согласующееся с опытом поведение во времени числа неустойчивых ядер, состоит в том, что распад любого из собрания одинаковых ядер равновероятен. Такое предположение естественно, поскольку различие вероятностей распада означало бы различие ядер, что противоречит исходному предположению. Следовательно, в соответствии с теремой Бернулли доля распадов N ядер есть вероятность распада каждого ядра. Так как распад происходит во времени, то и долю и вероятность относят к единице времени:

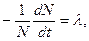
где λ – постоянная распада, имеющая смысл вероятности распада в единицу времени, а знак минус поставлен потому, что функция N(t) всегда убывающая. В другой записи:

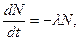(3.1)

т.е. число распадов пропорционально числу имеющихся ядер. Поскольку λ нормирована на время, то эта величина не обязательно меньше единицы, что имеет место для собственно вероятностей.

Решение уравнения (3.1) при начальном условии N(t=0)=N₀ дает:

N(t)=N₀ exp(-λt) (3.2)

Таким образом, число еще не распавшихся радиоактивных ядер уменьшается со временем по экспоненциальному закону (рис. 3.3).

Скорость распада J для любого момента времени может быть определена по соотношению:

J(t)=λN(t)=λN₀ exp(-λt)=J₀ exp(-λt) (3.3)

Таким образом постоянная распада является единственным параметром временных распределений.

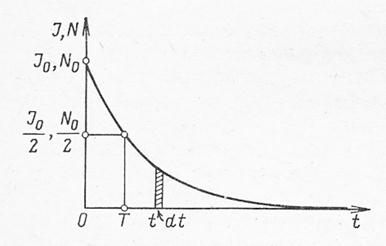
Рис. 3.3 Кривая радиоактивного распада

Характеристики распада. Среднее время жизни радиактивного нуклида может быть просто подсчитано исходя из соотношения (3.2). В соответствии с определением среднее время жизни равно сумме времен существования всех радиоактивных атомов, деленная на полное число радиоактивных нуклидов:

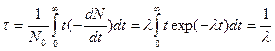(3.4)

Легко видеть, что среднее время жизни радиоактивного нуклида есть время, в течение которого число радионуклидов, а также скорость их распада уменьшаются в «е» раз.

На практике наиболее часто употребляется понятие «период полураспада Т_1/2». По определению период полураспада – это время в течение которого число радионуклидов или скорость их распада уменьшается в 2 раза, т.е.:

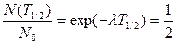, (3.5)

откуда

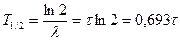(3.6)

Накопление активности. Если радионуклиды появляются в результате ядерной реакции, то их число в любой момент времени можно найти при условии, что известна скорость их образования. При известном сечении реакции σ и потоке частиц Ф число радионуклидов, возникающих в единице объема в единицу времениравно:

Q=Фσ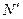, (3.7)

где 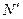- концентрация ядер-мишеней. С учетом рождения и распада радионуклидов их баланс в единицу времени в единице объема вещества в любой момент времени определяется соотношением:

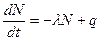(3.8)

Решением уравнения (3.8) является:

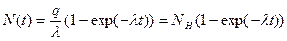, (3.9)

где N_Н – максимально возможное число радионуклидов – уровень пасыщения, который соответствует условию: число образующихся радионуклидов равно числу распадающихся (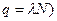, при этом dN/dt=0.

На рис. 3.4 показана кривые накопления и распада радионуклидов.

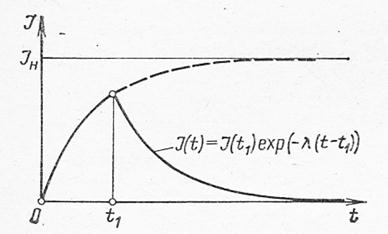
Рис. 3.4. Кривая накопления и распада радионуклидов.

Цепочка превращений. В результате распада радионуклида может образоваться как стабильны нуклид, так и радиоактивный. В последнем случае возникают цепочки распадов. Баланс радионуклидов при этом определяется уравнениями:

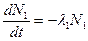
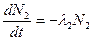
(3.10)

……………..

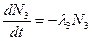
Решение для первого уравнения приведено выше (соотношение 3.2), решение для второго уравнения имеет вид:

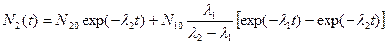, (3.11)

где N₁₀ и N₂₀ - число радионуклидов первого и второго сорта в начальный момент времени.

Для следующих членов цепочки решение еще более громоздкое.

Единицы активности. Активность радионуклида – это число распадов в единицу времени. Единицей активности является беккерель (Бк). Причем:

1 Бк = 1 расп/с

Ранее широко применялась единица активности кюри (Ки), причем:

1 Ки = 3,7.10¹⁰ Бк.

Такую активность имеет 1 г ²²⁶Ra.

Дата добавления: 2014-01-06