Альфа-распад

Условие распада. Альфа-распад характерен для тяжелых ядер, у которых а ростом А наблюдается уменьшение энергии связи, приходящейся на 1 нуклон. В этой области массовых чисел уменьшение числа нуклонов в ядре ведет к образованию более прочно связанного ядра. Однако выйгрыш в энергии при уменьшении А на единицу много меньше энергии связи одного нуклона в ядре, поэтому испускание протона или нейтрона, имеющего за пределами ядра энергию связи, равную нулю, невозможно. Испускание же ядра ⁴Не оказывается энергетичеки выгодным, так как удельная энергия связи нуклона в этом ядре около 7,1 МэВ. Альфа-распад возможен, если суммарная энергия связи ядра продукта и альфа-частицы больше, чем энергия связи исходного ядра. Или в массовых единицах:

M(A,Z)>M(A-4, Z-2) + M_α (3.12)

Увеличение энергии связи нуклонов означает уменьшение энергии покоя как раз на величину выделяющейся при альфа-распаде энергии Е_α. Поэтому, если представить альфа-частицу как целое в составе ядра-продукта, то она должна занимать уровень с положительной энергией, равной Е_α (рис. 3.5).

Рис. 3.5. Схема энергетического уровня альфа-частицы в тяжелом ядре

Когда альфа-частица покидает ядро, то эта энергия выделяется в свободном виде, как кинетическая энергия продуктов распада: альфа-частицы и нового ядра. Кинетическая энергия распределяется между этими продуктами распада обратно пропорционально их массам и, поскольку, масса альфа-частицы много меньше массы вновь образовавшегося ядра, практически вся энергия распада уносится альфа-частицей.. Таким образом, с большой точностью Е_α есть кинетическая энергия альфа-частицы после распада.

Однако, освобождению энергии препядствует кулоновский потенциальный барьер U_k (см. рисунок 3.5), вероятность прохождения которого альфа-частицей мала и очень быстро падает при уменьшении Е_α. Поэтому соотношение (3.12) не является достаточным условием альфа-распада.

Высота кулоновского барьера для заряженной частицы, проникающей в ядро или вылетающей из ядра, возрастает пропорционально ее заряду. Поэтому кулоновский барьер составляет еще большее препядствие для вылета из тяжелого ядра других прочно связанных легких ядер, таких как ¹²С или ¹⁶О. Средняя энергия связи нуклона в этих ядрах еще выше, чем в ядре ⁴Не, поэтому в ряде случаев испускание ядра ¹⁶О вместо последовательного вылета четырех альфа-частиц оказалось бы энергетически более выгодным. Однако испускание ядер более тяжелых, чем ядро ⁴Не, не наблюдается.

Объяснение распада. Механизм альфа-распада объясняет квантовая механика, т.к в рамках классической физики этот процесс невозможен. Только частица, обладающая волновыми свойствами, может оказаться за пределами потенциальной ямы при E_α<U_k. Более того, оказывается, что только потенциальный барьер бесконечно большой ширины с вероятностью равной единице, ограничивает пребывание частицы в пределах потенциальной ямы. Если же ширина барьера конечна, то вероятность перехода за пределы потенциального барьера принципиально всегда отлична от нуля. Правда эта вероятность быстро снижается с ростом ширины и высоты барьера. Аппарат квантовой механике приводит к следующему выражению для прозрачности барьера или вероятности ω оказаться частице за пределами потенциального барьера при столкновении с его стенкой:

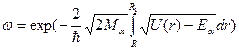(3.13)

Если представить альфа-частицу внутри сферической потенциальной ямы радиусом R, движущуюся со скоростью v_α, то частота ударов о стенки ямы составит v_α / R, и тогда вероятность вылета альфа-частицы из ядра на единицу времени, или постоянная распада, будет равна произведению числа попыток в единицу времени на вероятность прохождения барьера при одном столкновении со стенкой:

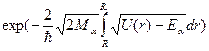, (3.14)

где - некоторый неопределенный коэффициент, поскольку были приняты положения, далекие от истины: альфа-частица не движется свободно в ядре, да и вообще в саставе ядер нет альфа-частиц. Она образуется из четырех нуклонов в момент альфа-распада. Величина имеет смысл вероятности образования в ядре альфа-частицы, частота столкновений которой со стенками потенциальной ямы равна v_α / R.

Сравнение с опытом. На основании зависимости (3.14) можно объяснить многие наблюдаемые при альфа-распаде явления. Период полураспада альфа-активных ядер тем больше, чем меньше энергия Е_α испускаемых при распаде альфа-частиц. Однако, если периоды полураспада меняются от долей микросекунды до многих миллиардов лет, то диапазон изменения Е_α очень мал и составляет примерно 4-9 МэВ для ядер с массовыми числами A>200. Регулярная зависимость периода полураспада от Е_α была давно обнаружена в опытах с естественными а-активными радионуклидами и описана соотношением:

(3.15)

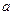где и 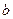- константы, несколько различающиеся для разных радиоактивных семейств.

Это выражение называется законом Гейгера-Нэттола и представляет степенную зависимость постоянной распада λ от Е_α с очень большим показателем 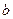. Такая сильная зависимость λ от Е_α непосредственно вытекает из механизма прохождения альфа-частицей потенциального барьера. Прозрачность барьера, а следовательно и постоянная распада λ зависят от интеграла по области R₁-R экспоненциально и быстро увеличиваются при росте Е_α. Когда Е_α приближается к 9 МэВ, время жизни по отношению к альфа-распаду составляет малые доли секунды, т.е. при энергии альфа-частиц 9 МэВ альфа-распад происходит практически мгновенно. Интересно, что такое значение Е_α еще существенно меньше высоты кулоновского барьера U_k, которая у тяжелых ядер для двухзарядной точечной частицы составляет примерно 30 МэВ. Барьер для альфа-частицы конечного размера несколько ниже и может быть оценен в 20-25 МэВ. Таким образом, прохождение кулоновского потенциального барьера альфа-частицей протекает весьма эффективно, исли ее энергия не ниже трети высоты барьера.

Прозрачность кулоновского барьера зависит также от заряда ядра, т.к. от этого заряда зависит высота кулоновского барьера. Альфа-распад наблюдается среди ядер с массовыми числами A>200 и в области A~150. Понятно, что кулоновский барьер при A~150 заметно ниже и вероятность альфа-распада для одинаковых Е_α значительно больше.

Хотя теоретически при любой энергии альфа-частицы существует вероятность проникновения через барьер, есть ограничения в возможности экспериментального определения этого процесса. Определить альфа-распад ядер с периодом полураспада больше 10¹⁷ – 10¹⁸ лет не удается. Соответствующее минимальное значение Е_α выше у более тяжелых ядер и составляет 4 МэВ у ядер с A>200 и около 2 МэВ у ядер с A~150. Следовательно выполнение соотношения (3.12) не обязательно свидетельствует о неустойчивости ядра по отношению к альфа-распаду. Оказывается, что соотношение (3.12) справедливо для всех ядер с массовыми числами больше 140, однако в области A>140 находится около одной трети всех встречающихся в природе стабильных нуклидов.

Границы устойчивости. Радиоактивные семейства. Границы устойчивости тяжелых ядер по отношению к альфа-распаду можно объяснить, используя модель ядерных оболочек. Ядра, имеющие только замкнутые протонные или нейтронные оболочки, являются особо прочно связанными. Поэтому, хотя энергия связи, приходящаяся на один нуклон, у средних и тяжелых ядер снижается при возрастании А, это снижение всегда замедляется при приближении А к магическому числу и ускоряется после прохождения А через магическое число протонов или нейтронов. В результате, энергия Е_α оказывается значительно ниже минимального значения, при котором наблюдается альфа-распад, для магических ядер или массовое число ядра меньше массового числа магического ядра. Напротив, энергия Е_α скачкообразно возрастает у ядер с массовыми числами, превышающими значения А магических ядер, и превосходит минимум практической стабильности а отношении альфа-распада.

В области массовых чисел A~150 альфа-активными являются нуклиды, ядра которых содержат на два ли несколько нейтронов больше магического числа 82. Некоторые из таких нуклидов имеют периоды полураспада много больше геологического возраста Земли и поэтому представлены в естественном виде – это нуклиды ¹⁴⁴Nd, ¹⁴⁷Sm, ¹⁴⁹Sm, ¹⁵²Gd. Другие были получены в результате ядерных реакций. Последние имеют недостаток нейтронов по сравнению со стабильными нуклидами соответствующих массовых чисел, и у этих нуклидов с альфа-распадом конкурирует обычно β⁺-распад. Самым тяжелым стабильным нуклидом является ²⁰⁹Bi, ядро которого содержит магическое число нейтронов 126. Предшествующий висмуту элемент свинец имеет магическое число протонов 82, а ²⁰⁸Pb является дважды магическим нуклидом. Все более тяжелые ядра радиоактивны.

Поскольку в результате альфа-распада ядро-продукт обогащается нейтронами, то после нескольких альфа-распадов следует бета-распад. Последний не меняет число нуклонов в ядре, поэтому любое ядро с массовым числом A>209 может превратиться в стабильное, только после некоторого числа альфа-распадов. Так как число нуклонов при альфа-распаде уменьшается сразу на 4 единицы, то возможно существование четырех независимых цепочек распада, каждая со своим конечным продуктом. Три из них представлены в природе и называются естественными радиоактивными семействами. Естественные семейства заканчивают свой распад образованием одного из изотопов свинца, конечным продуктом четвертого семейства является нуклид ²⁰⁹Bi (см. таблицу 3.1).

Существование естественных радиоактивных семейств обязано трем долгоживущим альфа-активным нуклидам – ²³²Th, ²³⁵U, ²³⁸U, имеющим периоды полураспада, сравнимые с геологическим возрастом Земли (5.10⁹ лет). Наиболее долгоживущим представителем вымершего четвертого семейства является нуклид ²³⁷Np – изотоп трансуранового элемента нептуния.

Таблица 3.1. Радиоактивные семейства

Семейство	Формула массового числа	Самый долгоживущий нуклид	Период полураспада, лет	Конечный продукт распада
Тория	4k	^232Th	1,39.10^10	^208Pb
Уран-актиния	4k-1	^235U	7,1.10^8	^207Pb
Уран-радия	4k-2	^238U	4,51.10^9	^206Pb
Нептуния	4k-3	^237Np	2,2.10^6	^209Bi

В настоящее время путем бомбардировки тяжелых ядер нейтронами и легкими ядрами получено очень много нуклидов, являющихся изотопами трансурановых элементов (Z>92). Все они неустойчивы и принадлежат к одному из четырех семейств.

Последовательнось распадов в естественных семействах показана на рис. 3.6. В тех случаях, когда вероятности альфа-распада и бета-распада оказываются сравнимыми, образуются вилки, которые соответствуют распадом ядер с испусканием либо альфа- либо бета-частиц. При этом конечный продукт распада остается неизменным.

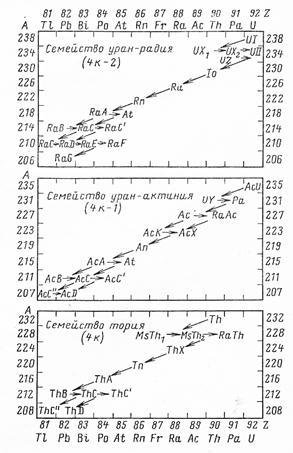
Рис. 3.6. Схемы распадов в природных семействах.

Приведенные наименования присвоены радионуклидам при первоначальном изучении естественных цепочек распада.

Дата добавления: 2014-01-06