Лекция 3. Тема: «Преобразование формул алгебры логики»

Тема: «Преобразование формул алгебры логики».

Постановка цели.

2) Устная работа.

Какие из следующих предложений не являются объектами алгебры логики:

Войдите!

река Волга длиннее реки Оби.

«Не курить!»

3*7>2*12

Пожалуйста, впустите!

Число 73 имеет 4 простых делителя.

Который час?

2) Даны высказывания А – «Петя едет в автобусе», В – «Петя читает книгу», С – «Петя смотрит в окно».

Составить формулы алгебры логики следующих сложных высказываний:

а) «Неверно, что Петя едет в автобусе и читает книгу».

б) «Неверно, что Петя едет в автобусе, читает книгу или смотрит в окно».

в) «Петя не едет в автобусе, но при этом читает книгу или смотрит в окно».

г) «Петя не едет в автобусе, не смотрит в окно – он читает книгу».

Решение:

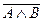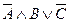а) ; б) ; в) ; г)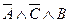

Используя основные законы алгебры логики можно одну формулу заменить другой, ей равносильной. Рассмотрим специальное преобразование формул, которое называется минимизацией формул алгебры логики.

Преобразование формулы алгебры логики в равносильное ей так, чтобы новая формула содержала наименьшее количество букв, называется минимизацией алгебры высказываний.

Упростить выражение:

1)

2)

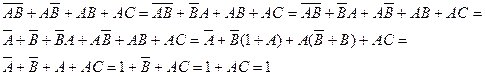
3)

4) Получите выражение, обратное данному:

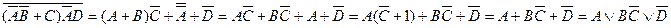
5) Используя закон де Моргана, преобразуйте формулы данных высказываний так, чтобы отрицание не распространялось на сложные высказывания. Если возможно, то упростите выражение.

а) ;

б) ;

в)

г) ;

д) ;

е) ;

ж)

з)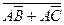

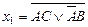6) Найти минимальные формулы высказываний:

;

;

.

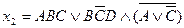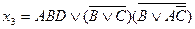7) Из простых высказываний (А – Виктор хороший пловец; В – Виктор хорошо ныряет; С – Виктор хорошо поет) составлена фраза, формула которой имеет вид: .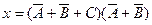

Установить равносильно ли высказывание Х высказыванию D-Виктор хороший пловец, и он хорошо поет.

8) Среди следующих высказываний выберите тождественно ложное:

9) Среди следующих высказываний выберите тождественно истинное:

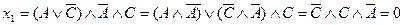
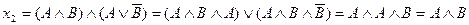
10) Данные высказывания запишите, используя только операции дизъюнкции и отрицания:

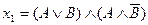
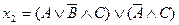
11) Запишите приведенные высказывания, используя только операции конъюнкции и отрицания:

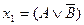
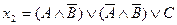
12) Какими высказываниями в каждом из II наборов равносильны:

1) ; ; ;

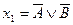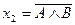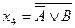
2) ; ;

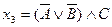
13) Даны высказывания:

а) «Сейчас идет дождь, а гром не гремит».

б) «Сейчас не идет дождь или сейчас гремит гром».

Как изменить второе высказывание, чтобы оно оказалось равносильно первому?

Контрольные вопросы.

1. Дайте определение логики.

2. Какие высказывания называются ложными, а какие истинными?

3. Какие логические связки существуют для составления сложных высказываний?

4. Какие высказывания называются тождественно истинными?

5. Какие законы алгебры логики используют для тождественных преобразований выражений?

Дата добавления: 2014-01-06