
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 2. Логика (от греческого слова «logos» - слово, мысль, речь, разум) – совокупность наук о законах и формах мышления
|
|
|
|
Тема: «Алгебра логики».
Логика (от греческого слова «logos» - слово, мысль, речь, разум) – совокупность наук о законах и формах мышления, о наиболее общих законах мышления. Начало исследований в области формальной логики было положено работами Аристотеля в IV веке до н.э. Логика оперирует понятиями, суждениями и умозаключениями. В середине XIX века возникли и начали интенсивно развиваться математические средства и методы. Именно она заложила теоретические основы последующей разработки языков программирования.
Одним из основных разделов математической логики является алгебра логики (исчисление высказываний), основоположником которой был Джордж Буль (1815-1864), положивший в основу своего логического учения методы алгебры (алгебра Буля).
1. Алгебра логики в современном изложении занимается исследованием операций с высказываниями.
Высказывание – это истинное или ложное предложение.
В естественном языке высказывания образуются повествовательным предложением или риторическим вопросом. Вопросительные и повелительные предложения не образуют высказывания. Высказывания могут быть истинными или ложными.
Например:
«истинные» - «Земля – планета Солнечной системы», «два умножить на два равно четыре», «три – простое число», «ребята – не Москва ль за нами»;
«ложные» - «Марс – не планета Солнечной системы», «пять меньше двух».
Предложения: «Будь осторожен!», «Справишься ли ты с заданием?» - не являются высказываниями.
Вопрос об истинности простых высказываний лежит вне сферы логики – на него отвечают конкретные науки, повседневная практика или наблюдения! Высказывания обычно обозначаются большими буквами латинского алфавита. Если высказывание А истинно, будем писать А=1, если ложно, то А=0.
Ложные высказывания содержат простые высказывания, соединенные логическими связками. А алгебре логики определены действия над высказываниями, выполняя которые, мы получаем новые сложные высказывания, истинность или ложность которых можно определить из таблицы истинности.
Логическая связка отрицание: в естественном языке ему соответствует выражение «неверно, что…», относящееся ко всему высказыванию, или присоединение союза «не» к некоторой части простого высказывания.
Например: если А – простое высказывание «Идет дождь», то отрицанием А (пишется: 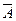 ) является высказывание «Неверно, что идет дождь» или «Дождь не идет». Отрицанию соответствует таблица истинности:
) является высказывание «Неверно, что идет дождь» или «Дождь не идет». Отрицанию соответствует таблица истинности:
| А | 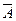
|
Логическая связка конъюнкция: в естественном языке ей соответствуют союзы «и», «а», «но», «но», «до», «однако», «хотя» и т.п. Возможны различные варианты записи конъюнкции: F=A^B; F=A*B; F=A&B, иногда даже знак конъюнкции опускается в сложное высказывание записывается следующим образом: F=AB. Иногда конъюнкцию называют логическим произведением.
| А | В | А^В |
Например: если А – «3-простое число» - истина; В – «3*2=6» - «истина»; то А^В: «3 – простое число и 3*2=6» - «истина».
Логическая связка дизъюнкция: в естественном языке ей соответствует союз «или», который может употребляться в двух разных смыслах: нестрогое «или» - когда члены дизъюнкции не исключают друг друга, то есть могут быть одновременно истинными, и строгое «или» (часто заменяется союзом «либо…, либо…») – когда члены дизъюнкции исключают друг друга.
Нестрогая дизъюнкция обозначается или F=A B; F=A+B.
B; F=A+B.
Нестрогая дизъюнкция: Сложные высказывания, получаемые из двух простых
| А | В | А В В
|
Например, если А – «Школьники в спортзале делают упражнения
на брусьях».
В – «Школьники в спортзале делают упражнения на турнике;
то A B – «Школьники в спортзале делают упражнения на брусьях
B – «Школьники в спортзале делают упражнения на брусьях
или на турнике».
Строгая дизъюнкция. Обозначается или F=A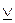 B, или F=A
B, или F=A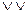 B, или F=A+B.
B, или F=A+B.
| А | В | А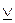 В В
|
Например, если А – «Школьники в спортзале играют в волейбол»,
В – «Школьники в спортзале играют в баскетбол;
то A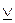 B – «Школьники в спортзале играют в волейбол или в
B – «Школьники в спортзале играют в волейбол или в
баскетбол».
2.Тождественные преобразования над высказываниями.
Истинность всякого сложного высказывания устанавливают с помощью таблиц истинности которые содержат всевозможные комбинации значений входных переменных вместе с соответствующими им значениями выходных переменных, то есть значения функций.
Высказывания, у которых совпадают таблицы истинности, называют равносильными. Составим следующую таблицу:
| А | В | А В В
| В А А
|
Из этой таблицы 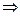 равносильность высказываний
равносильность высказываний
записанных формулами А В, В
В, В А. Для обозначения
А. Для обозначения
равносильности будем использовать знак =. Т.о.,
А В=В
В=В А.
А.
При тождественных преобразований формул алгебры логики можно заменять высказывания, входящие в формулу, равносильными.
| А | В | А В В
| В А А
|
Сложные высказывания, истинное для любых значений истинности, входящих в них простых высказываний, называются тождественно истинными.
Например, тождественно истинные формулы:
А
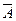 =1;
=1; 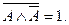
Тождественно ложными назовем формулы, принимающие значения 0 для любых значений истинности, входящих в него простых высказываний, например, А^А=0.
Например, В А
А
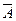 =В
=В 0
0
С (В
(В
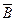 )=С
)=С 1
1
3. Свойства отдельных операций.
Операции конъюнкции:
А В=В В=В А.
(A А.
(A B) B) С=A С=A (B (B C)
A C)
A A=A
A A=A
A 1=A
A 1=A
A 0=0 0=0
| Операции дизъюнкции:
А В=В В=В А
A А
A (В (В С)= (A С)= (A B) B) C
A C
A A=A
A A=A
A 1=A
A 1=A
A 0=A 0=A
|
Отрицание: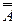 =А
=А
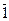 =0
=0
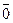 =1
=1
Взаимные распределительные свойства:
1. A (В
(В С)= A
С)= A B
B А
А C
C
A (В
(В С)= A
С)= A B
B C
C
2. A (В
(В С)= (A
С)= (A B)
B) (А
(А C)
C)
A (В
(В С)= A
С)= A B
B C
C
3. 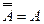
Формулы де Моргана:
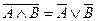
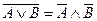
Применяя формулы Моргана, можно любую сложную формулу записать так, чтобы знак отрицания распространялся только на простые высказывания.
Например, 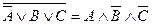 ,
,
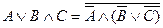
3. Законы алгебры логики.
1.Свойства опер. отрицания, конъюнкции и дизъюнкции:
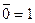 1=0
1=0
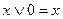
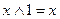
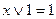
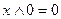
2. Закон идемпотентности:
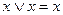
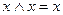
устанавливает, что повторяющиеся переменные в выражении излишни и их можно опустить, Т.о., понятие возведение в степень и умножение на коэффициенты, отличные от логических 0 и логических 1 (то есть числа, не имеют смысла.
3. Закон двойного отрицания.
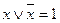
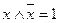
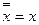
устанавливает, что дважды выполнение отрицание эквивалентно пустой операции.
4. Закон коммутативности:

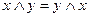
устанавливает, что порядок переменных при выполнении операций не влияет на результат этой операции.
5. Часто бывают полезны при упрощении булевых выражений следующие теоремы поглощения.

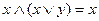
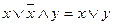
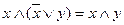
6. Закон де Моргана.
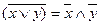
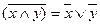
описывает эффект отрицания переменных, связанных операциями И и ИЛИ.
7. Согласно закону ассоциативности:
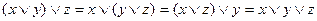

переменные можно группировать в любом порядке как для операций конъюнкции, так и для операций дизъюнкции.
8. Закон дистрибутивности:
х (у
(у z)=(x
z)=(x y)
y) (x
(x z) х
z) х (у
(у z)=(x
z)=(x y)
y) (x
(x z)
z)
устанавливает, что в алгебре логике допускается вынесение общего множителя за скобки.
9. Закон двойственности: (если Х - равносильно У, где Х и У – формулы указанного вида, то при замене в каждой из них всех знаков дизъюнкции на знак конъюнкции и наоборот, символа 1 на 0 и наоборот, равносильность сохраняется.
Например: из равносильности
A (В
(В С)= (A
С)= (A B)
B) (А
(А C) вытекает
C) вытекает
A (В
(В С)= (A
С)= (A B)
B) (А
(А C)
C)
Из равносильности: 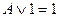 , вытекает
, вытекает 
Контрольные вопросы.
- Дайте определение логики.
- Какие высказывания называются ложными, а какие истинными?
- Какие логические связки существуют для составления сложных высказываний?
- Какие высказывания называются тождественно истинными?
- Какие законы алгебры логики используют для тождественных преобразований выражений?
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 878; Нарушение авторских прав?; Мы поможем в написании вашей работы!