П. 1. Системы счисления

Тема 8. Арифметические и логические основы ЭВМ

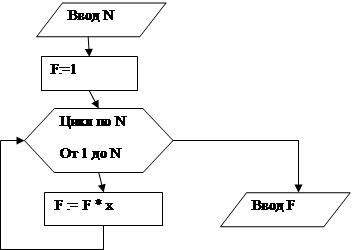
П. 7.2.2. Вычисление факториала числа N

П. 7.2.1. Найти сумму элементов массива A размера N

П. 7.2. Вычислительные алгоритмы.

Способ представления чисел посредством числовых знаков (цифр) называется системой счисления.

Правила записи и действий над числами в системах счисления, используемых в цифровой вычислительной технике, определяют арифметические основы цифровых ЭВМ.

Различают два основных вида систем счисления:

• непозиционные
• позиционные.

В непозиционной системе счисления значение числа определяется только конфигурацией цифровых символов.

Классическим примером непозиционной системы является римская система счисления.

В позиционных системах счисления значение любой цифры определяется не только конфигурацией ее символа, но и местоположением (позицией), которое она занимает в числе.

Основание позиционной системы счисления q есть количество различных цифр, используемых для представления числа.

Среди позиционных систем различают

• однородные
• смешанные системы счисления.

В однородных системах количество допустимых цифр для всех позиций (разрядов) числа одинаково.

Примером однородной позиционной системой является общепринятая десятичная система счисления (q=10), использующая для записи чисел десять цифр от 0 до 9.

Примером смешанной системы счисления может служить система отсчета времени, где в разрядах секунд и минут используется по 60 градаций, а в разрядах часов - 24 градации и т.д.

Любое число N, записанное в однородной позиционной системе может быть представлено в виде суммы ряда

где q - основание системы счисления (q≥2, целое положительное число);

ai - цифры системы счисления с основанием q (ai=0, 1, 2, …,q-1);

i - номер (вес) позиции (разряда) цифры (i=n,n-1,…,-m).

Принято представлять числа в виде последовательности соответствующих цифр (коэффициентов) разложения (1):

Запятая отделяет целую часть числа от дробной части.

В ВТ чаще всего для отделения целой части числа от дробной части используют точку.

Позиции цифр, отсчитываемые от точки, называют разрядами.

В позиционной СС вес каждого разряда отличается от веса (вклада) соседнего разряда в число раз, равное основанию СС.

В десятичной СС цифры 1-го разряда — единицы, 2-го — десятки, 3-го — сотни и т.д.

Может быть реализовано бесконечное множество различных систем счисления.

В цифровых вычислительных машинах в основном используются однородные позиционные системы

В ЭВМ находят широкое применение системы счисления с основанием, являющимся степенью числа 2, то есть двоичная, восьмеричная и шестнадцатеричная системы счисления.

При совместном использовании различных систем счисления число записывают в скобках и в качестве индекса указывают основание системы счисления.

Например,

(15)10; (1011)2; (735)8; (1EA9F)16.

Иногда скобки опускают и оставляют только индекс:

1510; 10112; 7358; 1EA9F16.

Есть еще один способ обозначения СС: при помощи латинских букв, добавляемых после числа.

Например,

15D; 1011B;735Q; 1EA9FH.

В таблице 1 приведены некоторые числа, представленные в различных СС.

Системы счисления
Десятичная q=10: цифры 0,1,2,…, 9	Двоичная q=2: цифры 0,1	Восьмеричная q=8: цифры 0,1,2,…, 6,7	Шестнадцатиричная q=16: 0,1,…,9,A,B,C,D,E,F
			А
			В
			С
			D
			E
			F

Дата добавления: 2014-01-06