Разыгрывание непрерывной случайной величины. Метод обратных функций

Пусть требуется разыграть непрерывную случайную величину X, т.е. получить последовательность ее возможных значений 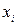(i=1, 2,..., n), зная функцию распределения F(x).

Теорема. Если 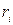- случайное число, то возможное значение 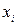разыгрываемой непрерывной случайной величины X с заданной функцией распределения F (х), соответствующее 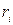, является корнем уравнения .

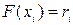Правило 1. Для того чтобы найти возможное значение 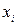, непрерывной случайной величины X, зная ее функцию распределения F (х), надо выбрать случайное число 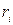, приравнять его функции распределения и решить относительно 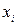полученное уравнение .

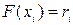Замечание 1. Если решить это уравнение в явном виде не удается, то прибегают к графическим или численным методам.

Пример 1. Разыграть 3 возможных значения непрерывной случайной величины X, распределенной равномерно в интервале (2, 10).

Решение: Напишем функцию распределения величины X, распределенной равномерно в интервале (а, b): .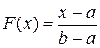

По условию, а=2, b=10, следовательно, .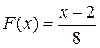

Используя правило 1, напишем уравнение для отыскания возможных значений 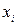, для чего приравняем функцию распределения случайному числу:

.

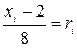Отсюда .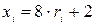

Выберем 3 случайных числа, например, 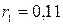, , 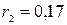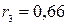. Подставим эти числа в уравнение, разрешенное относительно 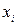; в итоге получим соответствующие возможные значения X: ; ; .

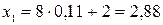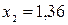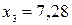Пример 2. Непрерывная случайная величина X распределена по показательному закону, заданному функцией распределения (параметр 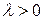известен) 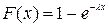(х >0). Требуется найти явную формулу для разыгрывания возможных значений X.

Решение: Используя правило, напишем уравнение .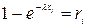

Решим это уравнение относительно 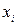: 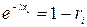, или .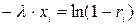

Отсюда .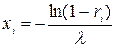

Случайное число 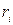заключено в интервале (0, 1); следовательно, число 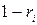- также случайное и принадлежит интервалу (0,1). Другими словами, величины R и 1-R распределены одинаково. Поэтому для отыскания 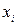можно воспользоваться более простой формулой .

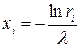Замечание 2. Известно, что .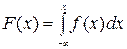

В частности, .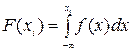

Отсюда следует, что если известна плотность вероятности 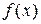, то для разыгрывания X можно вместо уравнений 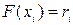решить относительно 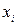уравнение .

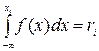Правило 2. Для того чтобы найти возможное значение 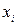непрерывной случайной величины X, зная ее плотность вероятности 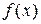, надо выбрать случайное число 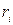и решить относительно 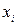уравнение 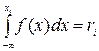или уравнение 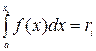, где а - наименьшее конечное возможное значение X.

Пример 3. Задана плотность вероятности непрерывной случайной величины X 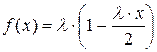в интервале 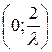; вне этого интервала 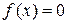. Требуется найти явную формулу для разыгрывания возможных значений X.

Решение: Напишем в соответствии с правилом 2 уравнение .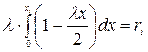

Выполнив интегрирование и решив полученное квадратное уравнение относительно 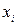, окончательно получим .

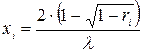18.7 Приближённое разыгрывание нормальной случайной величины

Напомним предварительно, что если случайная величина R распределена равномерно в интервале (0, 1), то ее математическое ожидание и дисперсия соответственно равны: М(R)=1/2, D(R)=1/12.

Составим сумму n независимых, распределенных равномерно в интервале (0, 1) случайных величин : .

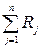Для нормирования этой суммы найдем предварительно ее математическое ожидание и дисперсию.

Известно, что математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Сумма 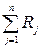содержит n слагаемых, математическое ожидание каждого из которых в силу М(R)=1/2 равно 1/2; следовательно, математическое ожидание суммы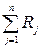

.

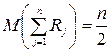Известно, что дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых. Сумма 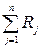содержит n независимых слагаемых, дисперсия каждого из которых в силу D(R)=1/12 равна 1/12; следовательно, дисперсия суммы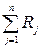

.

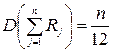Отсюда среднее квадратическое отклонение суммы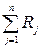

.

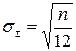Пронормируем рассматриваемую сумму, для чего вычтем математическое ожидание и разделим результат на среднее квадратическое отклонение: .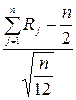

В силу центральной предельной теоремы при 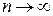распределение этой нормированной случайной величины стремится к нормальному с параметрами а=0 и 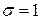. При конечном n распределение приближенно нормальное. В частности, при n=12 получим достаточно хорошее и удобное для расчета приближение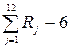

Правило. Для того чтобы разыграть возможное значение 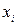нормальной случайной величины X с параметрами а=0 и 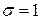, надо сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:

.

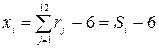Пример. а) Разыграть 100 возможных значений нормальной величины X с параметрами а=0 и 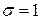; б) оценить параметры разыгранной величины.

Решение: а) Выберем 12 случайных чисел из первой строки таблицы, сложим их и из полученной суммы вычтем 6; в итоге имеем

.

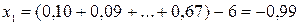Аналогично, выбирая из каждой следующей строки таблицы первые 12 чисел, найдем остальные возможные значения X.

б) Выполнив расчеты, получим искомые оценки:

, .

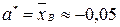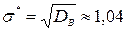Оценки удовлетворительные: 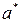близко к нулю, 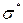мало отличается от единицы.

Список использованных источников

1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.:Высшая школа, 2001.

2. Калинина В.Н., Панкин В.Ф. Математическая статистика. – М.: Высшая школа, 2001.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2001.

4. Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика. – М.:ФОРУМ:ИНФРА-М, 2003.

5. Агапов Г.И. Задачник по теории вероятностей. – М.: Высшая школа, 1994.

6. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. – М.: ИНФРА-М, 2001.

7. Вентцель Е.С. Теория вероятностей. – М.: Высшая школа, 2001.

Дата добавления: 2014-01-06