Свойства проводника, потерями в котором нельзя пренебречь

Учет потерь в проводнике (R'¹0;G'¹0) при­водит, естественно, к затуханию волн. В этом случае волна напряжения, перемещающаяся в прямом на­правлении, имеет вид:

U(z,t)=U_e0(w)e^iwte^-gz (3.24)

Этому выражению соответствует решение телеграф­ного уравнения (3.13)

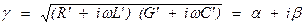(3.25)

Здесь g – коэффициент распространения, a – коэф­фициент затухания. Такое же выражение справедливо и для тока. Как и прежде, подставим решения для тока и напряжения в (5.38) и получим волновое со­противление Z, равное отношению напряжения и тока:

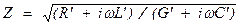(3.26)

Теперь волновое сопротивление – комплексная вели­чина, которая к тому же зависит от частоты. Если рассмотреть волну, отраженную от конца проводника, то получим выражение для коэффициента отражения. Он имеет такой же вид, как и для проводника, поте­рями в котором можно пренебречь (3.22). В проводниках, которые используют в измерениях и при передаче сигналов, потери обычно малы:

R' <<wL' и G'<<wС' (3.27)

При высоких частотах эти соотношения выполняются почти всегда. В этом случае волновое сопротивление становится действительным (Z=Zo), коэффициент распространения g можно вычислить, вынося за скоб­ки 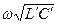, а для фазового коэффициента распро­странения и коэффициента затухания справедливы приближенные формулы

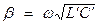(3.28)

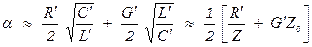(3.29)

Из (3.29) видно, что в этом случае сигналы распро­страняются с такой же скоростью 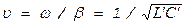, как и в проводнике, потерями в котором можно пре­небречь. В первом приближении эта скорость не за­висит от частоты, поскольку от частоты не зависят и значения погонных индуктивности и емкости. Значе­ния погонной емкости и индуктивности можно рассчи­тать, зная геометрические характеристики и физиче­ские свойства коаксиального кабеля [5.10]:

С^/=2pe_re₀/ln(D/d)=55,6e_r/ln(D/d) пф/м, (3.30)

L^/=(1/2p)m_rm₀ln(D/d)=200m_rln(D/d) нГн/м. (3.31)

Здесь e₀ – электрическая постоянная; e_r – относи­тельная диэлектрическая проницаемость диэлектрика; m₀ – магнитная постоянная; m_r – относительная маг­нитная проницаемость диэлектрика; d – диаметр внутреннего проводника; D – внутренний диаметр внешнего проводника. При m_r = 1 волновое сопротив­ление составит:

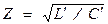=59.96(1/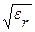)ln(D/d) Ом, (3.32)

а фазовая скорость будет равна:

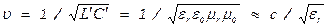(3.33)

В этом приближении фазовая скорость волн в коак­сиальном кабеле практически полностью определяется диэлектрической проницаемостью материала между двумя проводниками. Во многих высокочастотных кабелях для изоляции используют полиэтилен, ди­электрическая проницаемость которого e_r равна 2,28. В этом случае ясно, что фазовая скорость волн со­ставляет примерно 2/3 скорости света в вакууме с. Волновое сопротивление обычных коаксиальных ка­белей обычно составляет 50 и 75 Ом. Используются также кабели с сопротивлением 60, 95 и 120 Ом. Коэффициент затухания определяется путем сло­жения омических и диэлектрических потерь в провод­нике, которые по-разному зависят от частоты. Так, при высоких частотах имеем:

R' ~ 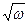и G' ~ w. (3.34)

Рост оптических потерь ограничивается при увеличении частоты тем, что при высоких частотах ток вы­тесняется во внешние слои проводника (так называе­мый скин-эффект). Поэтому при очень высоких частотах преобладают диэлектрические потери.

Передаточные свойства проводника длиной l, ко­торый соединен с волновым сопротивлением Zo, мож­но легко описать с помощью комплексной частотной характеристики H(w). [В технике связи характери­стику H(w) обычно называют передаточной функ­цией.] Из уравнений (3.24) и (3.25) получаем:

H(w) = Ua (t)/Ue (f) = U (l, t)/U (0, t)=e^-ale^-ibl=| H(w)|, (3.35)

фаза ф = - ibl = -wt_l определяется только временем пробега волн t_l, а амплитудная характеристика |H(w)| – коэффициентом затухания a и длиной про­водника l. Коэффициенты затухания можно найти в справочниках. Умножая найденное значение на дли­ну проводника l, можно получить логарифм ампли­тудной характеристики:

a (w) = (- 1/l) ln |Н (w) | = (1/l) ln (| Ue |/|Ua |) (3.36)

или

lg|H(w)| = - 0,434 a (w) l (3.37)

Хотя отношение амплитуд является безразмерной ве­личиной, для измерения логарифма этого отношения обычно пользуются «размерноподобной» единицей измерения [2.3]: логарифм отношения двух напряже­ний или токов измеряют в неперах (Нп). Таким об­разом, a (w) измеряется в единицах Нп/м:

a (w) =(1/{l}) ln (| Ue |/|Ua |), Нп/м. (3.38)

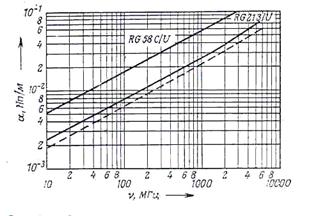
Рис. 5. Зависимость коэффициентов затухания a от частоты для коаксиальных кабелей RG58C/U и RG213/U. Штриховой линией показана частотная за­висимость коэффициента затухания для кабеля RG213/U, в котором в качестве изоляции исполь­зуется вспененный полиэтилен.

Здесь { l } численное значение длины проводника (в метрах). Для измерения десятичных логарифмов отношения мощностей сигналов была первоначально внедрена величина бел (Б). Однако на практике эту единицу стали использовать и для напряжений или токов. В этом случае обычно используют десятую часть единицы – децибел (дБ). Коэффициенты зату­хания, выраженные в Нп/м, можно перевести в деци­белы, пользуясь соотношением

1 Нп/м ==8,686 дБ/м. (3.39)

На рис. 5 приведена зависимость коэффициента затухания от частоты v для двух коаксиальных кабе­лей, широко применяемых в измерительной технике.

С помощью этих кривых можно определить верхнюю граничную частоту w_g, при которой отношение ампли­туд выходного и входного сигналов падает до 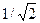. Из (3.36) получаем

a(w_g)=0,347/{l} Нп/м = 3,010/{l} дБ/м. (3.40)

Для примера, приведенного на рис. 5. коэффициен­ты затухания равны a(w_g)= 0,0315 Нп/м (б) и a(w_g)= 4,39-10^-3 Нп/м (в). Граничные частоты со­ставляют соответственно n_g ~310 МГц (б) и n_g ~7 МГц (в). Понятно, почему происходит такое сильное ослабление сигнала. Из рис. 2 видно, что если воспользоваться кабелем RG 213/U, то передача сигнала улучшится: при тех же длинах кабеля со­ответствующие граничные частоты составят n_g ~ 1450 МГц (б) и n_g ~ 33 МГц (в).

Дата добавления: 2014-01-06