Теплота

Работа

Работа (в механике) – произведение действующей на рабочее тело силы на путь ее действия.

Передачу энергии от одного тела к другому, связанную с изменением объема рабочего тела, с перемещением его во внешнем пространстве или с изменением его положения, называют работой.

В производстве работы всегда участвуют два тела или больше. Первое тело, производящее работу, отдает энергию, второе тепло получает энергию.

Определение работы расширения:

Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F.

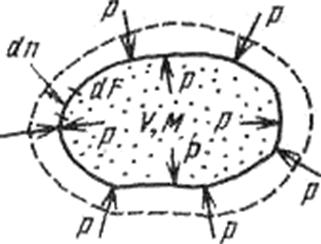
Рис. 1.2. К определению работы расширения

Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ действует на каждый элемент оболочки dF, с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя, данное выражение по всей поверхности F оболочки: 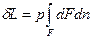(Различие символов δ и d у бесконечно малых величин 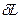и dU связано с тем, что величина 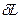в отличии от dU не является полным дифференциалом.)

Из рисунка видно, что изменение объема dV выражается в виде интеграла по поверхности: 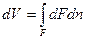, следовательно .

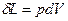При конечном изменении объема работа против сил внешнего давления, называемая работой расширения, равна

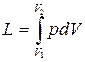. (1.7)

Отсюда следует, что 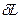и dV всегда имеют одинаковые знаки:

1) Если dV>0, то и 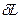>0, т.е. при расширении работа тела положительна, при этом тело само совершает работу;

2) Если же dV<0, то и 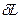<0, т.е. при сжатии работа тела отрицательна. Это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне.

Единицей измерения работы в СИ является джоуль (Дж).

Отнеся работу расширения к 1 кг массы рабочего тела, получим

; .

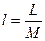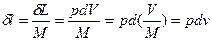Величина l, представляющая собой удельную работу, совершаемую системой, содержащей 1 кг газа, равна

.

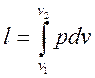Вышеперечисленные формулы справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.

В термодинамике для исследования равновесных процессов широко используют p,v-диаграмму. Поскольку состояние термодинамической системы определяется двумя параметрами, то на p,v диаграмме оно изображается точкой. На рис. 1.3 точка 1 соответствует начальному состоянию системы, точка 2 – конечному, а линия 1-2 процессу расширения рабочего тела от v₁ до v₂.

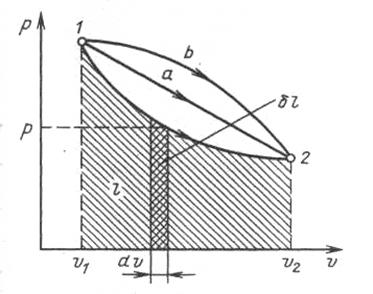
Рис. 1.3. Графическое изображение работы в

p,v- координатах

При бесконечно малом изменении объема dv площадь заштрихованной вертикальной полоски равна 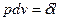. Следовательно, работа процесса 1-2 изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами. Таким образом, работа изменения объема эквивалентна площади под кривой процесса в диаграмме p,v.

Каждому пути перехода системы из состояния 1 в состояние 2 (например, 1-2, 1-а-2 или 1-b-2) соответствует своя работа расширения: l_1b2>l_1a2>l₁₂. Следовательно, работа зависит от характера термодинамического процесса, а не является функцией только исходного и конечного состояния системы. С другой стороны, 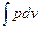зависит от пути интегрирования и, следовательно, элементарная работа δ l не является полным дифференциалом.

Поскольку величина δ l пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые обладают способностью значительно увеличивать свой объем (водяной пар в энергетике, газообразные продукты сгорания в ДВС).

Теплота – мера количества энергии, переданной микрофизическим путем (Дж).

Теплота может передаваться:

1) При непосредственном контакте между телами (теплопроводность, конвекция);

2) На расстоянии (излучение).

Во всех случаях этот процесс возможен только при наличии разности температур между телами.

Элементарное количество теплоты δ Q, так же как и 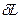, не является полным дифференциалом, в отличии от дифференциала внутренней энергии dU.

Внутренняя энергия – это свойство самой системы, она характеризует состояние системы. Теплота и работа – это энергетические характеристики процессов механического и теплового взаимодействий системы с окружающей средой. Они характеризуют те количества энергии, которые переданы системе или отданы ею через ее границы в определенном процессе.

Дата добавления: 2014-01-06