
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Относительность механического движения. Системы отсчета
|
|
|
|
Кинематика
Механическое движение - это изменение положения тел в пространстве относительно друг друга с течением времени.
Механическое движение может быть прямолинейным или криволинейным, равномерным или неравномерным.
Материальная точка - это тело, размеры и форму которого при решении задачи можно не учитывать.
Условия, при выполнении которых тело можно считать материальной точкой:
1. если его размеры малы по сравнению с расстоянием, которое оно проходит.
2. если оно движется поступательно.
Что такое поступательное движение?
Тело движется поступательно, если все его точки движутся одинаково.
или тело движется поступательно, если прямая, проведенная через две точки этого тела, при его перемещении смещается параллельно своему первоначальному положению.
Системо отсчета (СО)
Тело отсчета, связанная с ним система координат и часы для отсчета времени движения образуют систему отсчета.
Тело отсчета - это тело, относительно которого определяется положение других (движущихся) тел.
Относительность движения
Человек идет по вагону против движения поезда (рис. 1). Скорость поезда относительно поверхности земли равна 20 м/с, а скорость человека относительно вагона равна 1 м/с. Определите, с какой скоростью и в каком направлении движется человек относительно поверхности земли.

Будем рассуждать так. Если бы человек не шел по вагону, то он переместился бы вместе с поездом на расстояние, равное 40 м. Но за это же время он прошел расстояние, равное 1 м, против хода поезда. Поэтому за время, равное 1 с, он сместился относительно поверхности земли только на 19 м в направлении движения поезда. Значит, скорость человека относительно поверхности земли равна 19 м/с и направлена в ту же сторону, что и скорость поезда. Таким образом, в системе отсчета, связанной с поездом, человек движется со скоростью 1 м/с, а в системе отсчета, связанной с каким-либо телом на поверхности земли, — со скоростью 19 м/с, причем направлены эти скорости в противоположные стороны. Мы видим, что скорость относительна, т. е. скорость одного и того же тела в разных системах отсчета может быть различной как по числовому значению, так и по направлению.

Теперь обратимся к другому примеру. Представьте вертолет, вертикально опускающийся на землю. Относительно вертолета любая точки винта, например точка А (рис. 2), будет все время двигаться по окружности, которая на рисунке изображена сплошной линией. Для наблюдателя, находящегося на земле, та же самая точка будет двигаться по винтовой траектории (штриховая линия). Из этого примера ясно, что траектория движения тоже относительна, т. е. траектория движения одного и того же тела может быть различной в разных системах отсчета.
Отсюда следует, что и путь является величиной относительной, ведь путь — это сумма длин всех участков траектории, пройденных телом за рассматриваемый промежуток времени. Это особенно наглядно проявляется в тех случаях, когда физическое тело движется в одной системе отсчета и покоится в другой. Например, человек, сидящий в движущемся поезде, проходит определенный путь s в системе, связанной с Землей, а в системе отсчета, связанной с поездом, его путь равен нулю.
Таким образом, относительность движения, проявляется в том, что скорость, траектория, путь и некоторые другие характеристики движения относительны, т. е. они могут быть различны в разных системах отсчета.
| Относительность механического движения. | |
| 1. Механическое движение можно наблюдать только относительно других тел. Обнаружить изменение положения тела, если не с чем сравнивать невозможно. 2. В различных системах отсчета физические величины (скорость, ускорение, перемещение и т.д.), характеризующие движение одного и того же тела, могут быть различными. 3. Характер движения, траектория движения и т.п. различны в разных системах отсчета для одного и того же тела. | |
Пусть две СО движутся друг относительно друга с постоянной скоростью 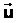 . Положение точки А в неподвижной системе К задано вектором . Положение точки А в неподвижной системе К задано вектором  , а в движущейся системе К1 - вектором , а в движущейся системе К1 - вектором 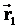 . Из чертежа видим, что . Из чертежа видим, что  . Это уравнение позволяет переходить из одной СО в другую.
При этом мы считаем, что время течет в обеих СО одинаково.
Будем условно называть систему К неподвижной, а систему К1 - движущейся. . Это уравнение позволяет переходить из одной СО в другую.
При этом мы считаем, что время течет в обеих СО одинаково.
Будем условно называть систему К неподвижной, а систему К1 - движущейся.
| 
|
Тогда для случая, когда координаты y и z не меняются, получим:
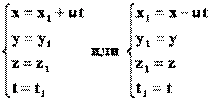 - преобразования Галилея. - преобразования Галилея.
| |
Из этих уравнений следует:
- расстояние между двумя точками абсолютно, т.е. не зависит от выбора СО. Пусть в неподвижной СО координаты точек x и x', а в подвижной соответственно x1 и x1'. Тогда 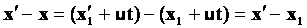 ; ;
 Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение.
Получим:
Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение.
Получим:  - закон сложения скоростей.Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной.
- закон сложения скоростей.Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной.
| 
|
| Скорость подвижной СО относительно неподвижной наз. переносной скоростью. | |
| При решении задач часто бывает удобно принимать одно из движущихся относительно Земли тел за неподвижное. Тогда скорость Земли в этой СО будет равна по величине и противоположна по направлению скорости данного тела. | |
Если скоростиv1 и u сонаправлены, то их проекции складываются, если противоположно направлены (тела удаляются) – вычитаются.
Если скорости направлены под прямым углом - 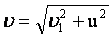 если угол произвольный, то необходимо пользоваться теоремой косинусов: если угол произвольный, то необходимо пользоваться теоремой косинусов: 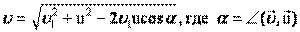 . .
| |
| Эти выводы справедливы для скоростей много меньших скорости света в вакууме (3.108м/с). |
4. Характеристики механического движения: скорость, ускорение, перемещение
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:
vcp = vСкорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела 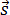 за любой промежуток времени к значению этого промежутка t:
за любой промежуток времени к значению этого промежутка t:
 =
= 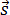 / t
/ t
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
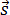 =
=  • t
• t
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:
Проекция перемещения на ось ОХ равна:
s = vt = x – x0где x0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:
х = x0 + vtЕсли положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
х = x0 - vt
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / tМгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
 =
= 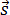 '
'
Проекция вектора скорости на ось ОХ:
vx = x’это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
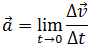
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
 =
=  ' =
' = 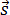 "
" Учитывая, что  0 – скорость тела в начальный момент времени (начальная скорость),
0 – скорость тела в начальный момент времени (начальная скорость),  – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
– скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
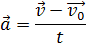
Отсюда формула скорости равнопеременного движения в любой момент времени:
 =
=  0 +
0 +  t
t Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x + axtТак как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t.
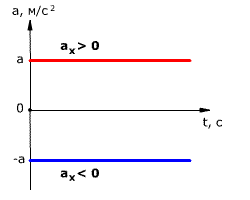
Рис. 1. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 2)

Рис. 2. Зависимость скорости тела от времени.
При этом перемещение численно равно площади фигуры 0abc (рис.2).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0bc = vВысота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
 ;
; 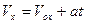 ;
; 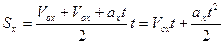
Общая формула для определения проекции перемещения:
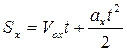
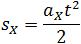 , Vox = 0
, Vox = 0
Если неизвестно время, то 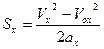
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 5145; Нарушение авторских прав?; Мы поможем в написании вашей работы!