Абсолютная и условная сходимость рядов

Определение 3. Ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин членов данного ряда, т.е. если сходится ряд .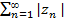

Определение 4. Ряд называется условно сходящимся, если данный ряд сходится, а ряд 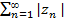, составленный из модулей членов данного ряда расходится.

Примером абсолютно сходящегося ряда может служить ряд . В самом деле, ряд из модулей членов данного ряда 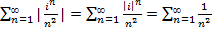является рядом Дирихле S=2>1, который сходится.

Примером условно сходящегося ряда может служить ряд . В примере 1 показано, что рассматриваемый ряд сходится. Рассмотрим ряд, составленный из модулей членов данного ряда, , который расходится. Следовательно, ряд сходится условно.

Дата добавления: 2014-01-06