
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нахождение круга сходимости степенного ряда
|
|
|
|
Степенные ряды с комплексными членами. Теорема Абеля. Нахождение круга сходимости степенного ряда.
Ряд вида 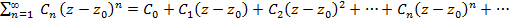 , где
, где 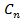 - комплексные числа,
- комплексные числа,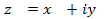 ,
,  , называется степенным рядом с комплексными членами.
, называется степенным рядом с комплексными членами.
Теорема Абеля. Если степенной ряд 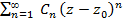 сходится в точке
сходится в точке 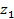 ,
, 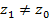 , то он сходится и при том абсолютно в круге
, то он сходится и при том абсолютно в круге 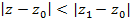 .
.
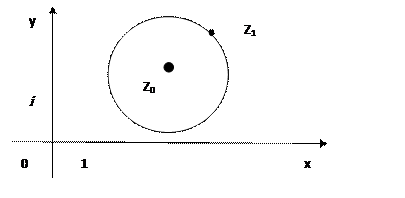
Рассмотрим ряд 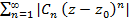 , который составлен из модулей членов данного ряда. Полученный ряд является знакоположительным рядом, и к нему можно применить либо признак Даламбера, либо признак Коши.
, который составлен из модулей членов данного ряда. Полученный ряд является знакоположительным рядом, и к нему можно применить либо признак Даламбера, либо признак Коши.
Вначале применим признак Даламбера, т.е. найдем
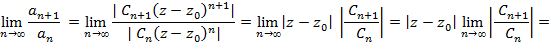
 .
.
Это означает, что данный ряд сходится в круге 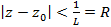 с центром в точке
с центром в точке 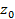 радиуса R,а вне этого круга ряд расходится. В точках окружности
радиуса R,а вне этого круга ряд расходится. В точках окружности 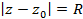 ряд может сходиться, а может и расходиться.
ряд может сходиться, а может и расходиться.
Теперь к ряду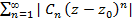 применим признак Коши.
применим признак Коши.
Найдем предел 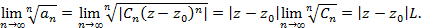
Если 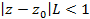 , то ряд сходится, а если
, то ряд сходится, а если 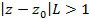 , то ряд расходится.
, то ряд расходится.
Следовательно, данный ряд сходится в круге 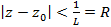 с центром в точке
с центром в точке 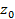 радиуса R,а вне этого круга ряд расходится. В точках окружности
радиуса R,а вне этого круга ряд расходится. В точках окружности 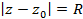 ряд
ряд 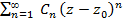 может сходиться, а может и расходиться.
может сходиться, а может и расходиться.
Пример 2. Найти круг сходимости степенного ряда 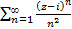 и исследовать сходимость ряда на границе круга сходимости.
и исследовать сходимость ряда на границе круга сходимости.
Решение. Рассмотрим ряд 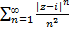 , к которому применим признак Коши. Найдем
, к которому применим признак Коши. Найдем 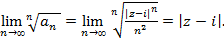 При
При 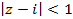 ряд сходится, а при
ряд сходится, а при 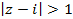 расходится. Следовательно,
расходится. Следовательно, 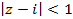 является кругом сходимости с центром в точке
является кругом сходимости с центром в точке  и радиуса 1.
и радиуса 1.
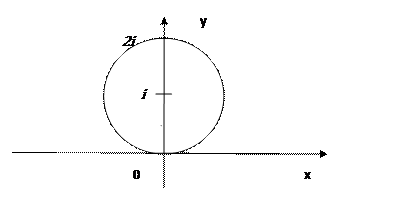
Возьмем произвольную точку 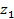 на границе круга сходимости, т.е.
на границе круга сходимости, т.е. 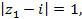 и рассмотрим данный степенной ряд в точке
и рассмотрим данный степенной ряд в точке 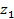 , т.е. ряд
, т.е. ряд 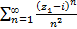 , который проверим на абсолютную сходимость. Для этого рассмотрим ряд, составленный из модулей членов последнего ряда, т.е. рассмотрим ряд
, который проверим на абсолютную сходимость. Для этого рассмотрим ряд, составленный из модулей членов последнего ряда, т.е. рассмотрим ряд 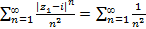 , который сходится. Следовательно, ряд
, который сходится. Следовательно, ряд  в каждой точке окружности
в каждой точке окружности 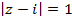 сходится абсолютно.
сходится абсолютно.
10.5. Определение функций  Формулы Эйлера.
Формулы Эйлера.
Известно, что
 (1)
(1)
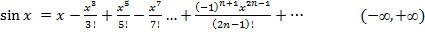 (2)
(2)
 (3)
(3)
Положим:
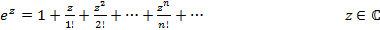 (4)
(4)
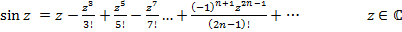 (5)
(5)
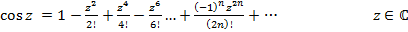 (6)
(6)
Если в рядах (4),(5),(6) положить z=x, то получим соответственно ряды (1),(2),(3). Это означает, что функции  на действительной прямой z=x совпадают соответственно с ранее определенными функциями
на действительной прямой z=x совпадают соответственно с ранее определенными функциями 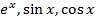 .
.
Покажем, что функции  определены на всей комплексной плоскости. Для этого надо показать, что ряды (4),(5),(6) сходятся во всей комплексной плоскости.
определены на всей комплексной плоскости. Для этого надо показать, что ряды (4),(5),(6) сходятся во всей комплексной плоскости.
Ряды (4),(5),(6) являются степенными, поэтому нам достаточно показать, что радиусы сходимости этих рядов равны .
.
Например, найдем радиус сходимости ряда (4). Рассмотрим ряд из модулей членов ряда (4), т.е. ряд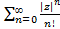 и применим к этому ряду признак Даламбера.
и применим к этому ряду признак Даламбера.

Так как 0<1 для любого Z, то ряд (4) сходится абсолютно, а, следовательно, сходится на всей комплексной плоскости, R= . Аналогично доказывается, что ряды (5) и (6) сходятся на всей комплексной плоскости.
. Аналогично доказывается, что ряды (5) и (6) сходятся на всей комплексной плоскости.
Теперь рассмотрим функцию
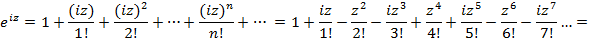
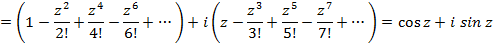
Итак, получена формула 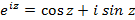 , которая называется формулой Эйлера.
, которая называется формулой Эйлера.
Из формулы Эйлера можно получить следующие формулы:

Отметим, что 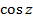 является четной функцией, а
является четной функцией, а  – нечетной функцией.
– нечетной функцией.
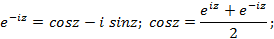
 .
.
Пользуясь формулами Эйлера, можно доказать, что функция 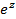 является периодической с периодом
является периодической с периодом 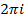 , а функции
, а функции 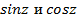 тоже являются периодическими с периодом
тоже являются периодическими с периодом 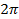 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 8528; Нарушение авторских прав?; Мы поможем в написании вашей работы!