Предел, непрерывность, производная функции комплексного переменного

Пусть функция w=f(z) определена и однозначна в некоторой окрестности точки 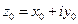, кроме, быть может самой точки .

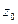Будем говорить, что предел функции w=f(z) существует при 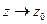, если существуют оба предела 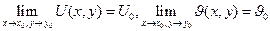, при этом будем полагать: .

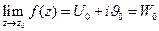Так как определение предела функции f(z) сводится к определению предела действительных функций, то теоремы о пределе суммы, произведения, частного сохраняются и для функций комплексного переменного.

Определение 2: Определение предела функции комплексного переменного можно сформулировать и с помощью понятия окрестности.

Число 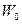называется пределом функции W=f(z) в точке 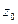, если , то . Отметим, что f(z) стремится к 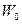независимо от способа приближения точки z к 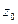. Таким образом, если 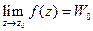, то при стремлении z к 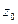по какой-либо линии, f(z) будет стремиться к .

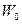Определение 3: Пусть функция W=f(z) определена в некоторой окрестности точки 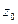(включая саму точку 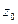). Функция W=f(z) называется непрерывной в точке 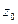, если предел функции в точке 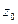равен значению функции в этой точке, т.е. .

Отметим, для того, чтобы функция f(z)=U(x,y)+ 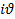(x,y) была непрерывной в точке 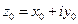необходимо и достаточно, чтобы обе функции U(x,y) и 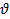(x,y) были непрерывны в точке .

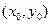Так как определение непрерывности функции комплексного переменного аналогично определению непрерывности функции действительного переменного, то теоремы о непрерывности суммы, произведения, частного остаются справедливыми и для функций комплексного переменного.

Определение 4: Пусть f(z) определена в некоторой окрестности точки z, включая саму точку z. Производной функции f(z) в точке z называется предел:

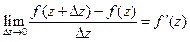
В этом случае говорят, что функция f(z) дифференцируема в точке z.

Условия дифференцируемости функции f(z)=U(x,y)+ 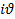(x,y) в терминах действительных функций U(x,y) и 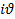(x,y) выражаются в следующей теореме:

Теорема. (Условия Коши-Римана)(Эйлера-Даламбера).

Пусть f(z)=U(x,y)+ 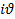(x,y) определена в некоторой окрестности точки z, причем U(x,y) и 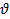(x,y) непрерывны в точке z вместе со своими частными производными первого порядка. Для того, чтобы f(z) имела в точке z производную (f(z) была дифференцируема в точке z) необходимо и достаточно выполнение условий:

(условия Коши-Римана).

Доказательство.

Необходимость. Дано: f(z) в точке z имеет производную. Требуется доказать, что выполняются равенства . Так как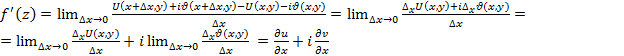

Далее, положим, что 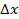=0, тогда 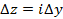. Отсюда следует равенство

Так как обычные свойства алгебраических действий и предельного перехода сохраняются при переходе к функциям комплексного переменного, то сохраняются обычные правила дифференцирования.

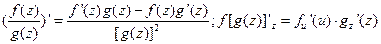, где u=g(z); 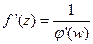, где f(z) и 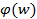взаимно обратные функции.

C учетом условий Коши-Римана, производную f’(z) можно находить по формуле: .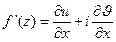

Определение 5. Функция называется аналитической в области, если она имеет производную в каждой точке этой области.

Отметим, что понятие аналитической функции относится только к однозначным функциям, т.к. понятие предела и производной было дано для однозначных функций.

Пример 1. Проверить выполнение условий Коши-Римана для функции и найти ее производную.

Решение.

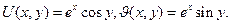
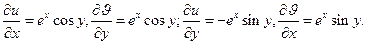
Следовательно, , кроме этого отметим, что U(x,y) и 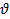(x,y) непрерывны вместе со своими частными производными первого порядка на всей плоскости. Таким образом, условия Коши-Римана выполняются. Производную найдем по формуле:

.

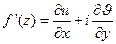Дата добавления: 2014-01-06