Колебания автомобиля

Кузов автомобиля имеет шесть степеней свободы и совершает весьма различные колебания (рис. 50.). Линейные перемещения вдоль осей х и у: S_х – подергивание, S_у – шатание, S_z – подпрыгивание, и угловые перемещения вокруг этих осей a_х – покачивание, a_у – галопирование, a_z – виляние.

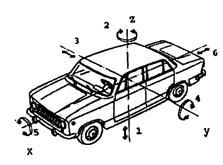
Рис. 50. Основные виды колебаний

Приведенная жесткость подвески (с_п) складывается из жесткости упругих элементов самой подвески (c_р) и жесткости пневматических шин (c_ш) (рис. 51.).

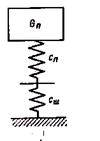
Рис. 51. Определение приведенной жесткости подвески

Под влиянием веса G_п упругая система деформируется на величину, равную сумме прогибов подвески и шины. Вместе с тем суммарный прогиб этой системы, который определяют по изменению положения оси колеса:

f = G_п/с_пр, (193)

где с_пр – приведенная жесткость подвески и шины, Н/м.

Тогда

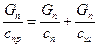. (194)

Решив полученное равенство получим:

с_пр = 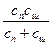. (195)

Жесткость передней или задней подвески современных автомобилей находится в пределах 20 - 60 кН/м, а жесткость шин – в пределах 200 - 450 кН/м.

Для уменьшения вертикальных колебаний используют мягкую подвеску и устанавливают амортизаторы. Чтобы иметь представление о том, каким образом уменьшить галопирование, познакомимся с понятием о центре упругости системы /3/. Центром упругости системы называют точку, при приложении к которой внешней возмущающей силы возникает только линейное перемещение системы. Рассмотрим стержень, который опирается на упругие элементы подвески (рис. 52).

Если сила Р приложена не к центру упругости, то происходит линейное и угловое перемещение стержня (положение 1). Если сила Р приложена к центру упругости, то происходит только линейное перемещение стержня(положение 2). В последнем случае f₁ = f₂, вследствие чего

галопирование отсутствует.

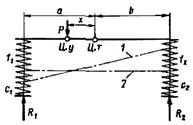
Рис. 52 Определение положения центра упругости

Определим величину х – расстояние от центра упругости до центра тяжести из условия равновесия стержня:

åМ_цт = R₁a – Px – R₂b = 0. (196)

Решив относительно х, получим:

х = (R₁a – R₂b)/Р. (197)

Заменим реакции R₁ и R₂ произведениями R₁ = с₁f₁ и R₂ = с₂f₂, следовательно Р = R₁ + R₂, откуда:

х = 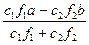. (198)

Но по условию f₁ = f₂, то:

х = 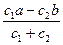. (199)

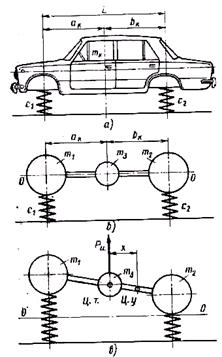
Применим данное выражение к колебаниям кузова, заменив подрессоренную массу кузова m_к тремя массами, связанными между собой невесомым стержнем (рис. 53,б).

Рис. 53. Свободные колебания кузова

Чтобы система соответствовала в динамическом отношении действительной массе подрессоренной части автомобиля, необходимо соблюдение следующих условий:

1.сумма всех масс системы должна быть равна подрессоренной массе автомобиля:

m₁ + m₂ + m₃ = m_к. (200)

2. центр тяжести системы должен совпадать с центром тяжести кузова:

m₁а_к = m₂b_к. (201)

3. момент инерции системы относительно горизонтальной оси у должен равняться моменту инерции подрессренной массе авиомобиля относительно той же оси:

m₁а_к² + m₂b_к² = I = m_кr_к², (202)

где r_к – радиус инерции подрессоренной массы автомобиля.

Из уравнений (200) – (202) определим массы m₁, m₂, m₃:

m₁ = (m_кr_к²)/(а_кL); (203)

m₂ = (m_кr_к²)/(b_кL); (204)

m₃ = m_к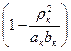. (205)

Если стержень вывести из состояния равновесия, а затем отпустить, то он начнет колебаться (рис. 53,в). во время колебаний появляется сила инерции:

Р_и = m₃j. (206)

Она создает момент относительно центра упругости:

М_и = Р_их = m₃jх. (207)

М_и = 0, если m₃ = 0 или когда х = 0. Из уравнения следует, что m₃ = 0, если r_к²/(а_кb_к) = 1, т. к. m_к ¹ 0.для легковых автомобилей отношение r_к²/(а_кb_к) близко к единице, вследствии чего они имеют хорошую плавность хода.

Если плечо х = 0 и центр тяжести совпадает с центром упругости, то:

х = 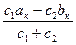= 0. (208)

тогда с₁а_к = с₂b_к или с₁/с₂ = b_к/а_к.

Дата добавления: 2014-01-06