Геометрические характеристики плоских сечений

Лекция 4

Простейшая геометрическая характеристика плоской фигуры – её площадь. От площади поперечного сечения зависят прочность и жесткость стержня при осевом растяжении и сжатии.

При изучении изгиба, кручения, различных случаев работы стержня на сложное сопротивление, а также при расчетах сжатых стержней на устойчивость приходится встречаться с более сложными геометрическими характеристиками плоских сечений: статическими моментами, моментами инерции, моментами сопротивления, радиусами инерции.

Геометрические характеристики сечений простой формы могут быть вычислены по соответствующим формулам. В таблицах ГОСТа приводятся геометрические характеристики профилей стандартного проката: равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков, двутавров (ГОСТ 8239-89), швеллеров (ГОСТ 8240-89). Для вычисления геометрических характеристик сечений сложной формы их приходится расчленять на ряд простых фигур и пользоваться формулами, устанавливающими зависимость между геометрическими характеристиками относительно различных осей.

Рассмотрим основные свойства и методы вычисления геометрических характеристик плоских сечений.

СТАТИЧЕСКИЕ МОМЕНТЫ ПЛОЩАДИ СЕЧЕНИЯ.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ СЕЧЕНИЯ

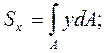
Статическим моментом площади сечения относительно некоторой оси называется, взятая по всей его площади A сумма произведений элементарных площадок dA на расстояние до соответствующей оси (рис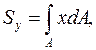.4.1):

(4.1)

где 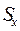- статический момент площади сечения относительно оси x;

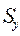- статический момент площади сечения относительно оси y.

Размерность статического момента – (ед. длины)³, например, мм³, см³, м³.

Если уподобить сечение однородной пластинке, то нетрудно установить тождественность определения статического момента площади сечения и момента силы тяжести этой пластинки. Используя теорему о равнодействующей, можно получить удобную для расчетов формулу вычисления статического момента простой фигуры:

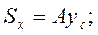
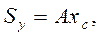(4.2)

где 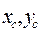- координаты центра тяжести сечения.

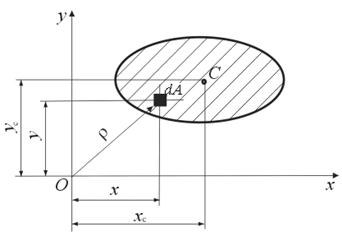
Рис. 4.1

Если сечение имеет сложное очертание, то для определения статических моментов используется интегральная формула (4.1). Статический момент площади сечения может быть положительным, отрицательным, равным нулю в зависимости от положения оси, относительно которой он вычисляется. Ось, проходящая через центр тяжести сечения, называется центральной.

Для определения статического момента сложного сечения его расчленяют на отдельные простые фигуры (рис.4.2). На основании главного свойства интеграла статический момент сложного сечения равен сумме статических моментов составляющих его простых фигур:

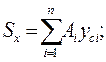
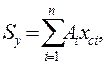(4.3)

где 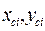- координаты центра тяжести i -й простой фигуры.

Исходя из выражений (4.2) и (4.3), получаем формулы для нахождения координат центра тяжести сложного сечения, состоящего из n простых фигур:

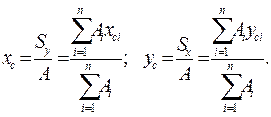(4.4)

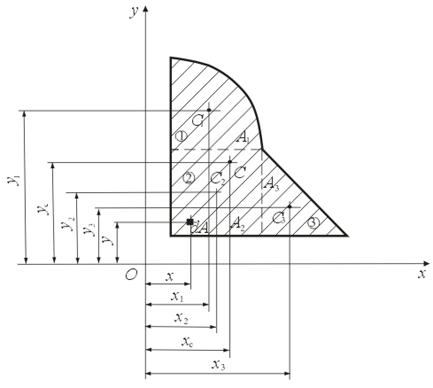
Рис. 4.2

Из сказанного можно сделать следующий вывод: если какая-либо ось проходит через центр тяжести сечения, то статический момент площади сечения относительной этой оси равен нулю; и наоборот, если статический момент относительно какой-либо оси обращается в нуль, то эта ось является центральной.

ПОНЯТИЕ О МОМЕНТАХ ИНЕРЦИИ СЕЧЕНИЯ

Осевым моментом инерции сечения относительно данной оси называется взятая по всей площади сечения сумма произведений элементарных площадок на квадраты их расстояний до этой оси (см. рис. 4.1):

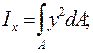
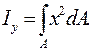(4.5)

Полярным моментом инерции сечения относительно некоторой точки (полюса 0) называется взятая по всей его площади сумма произведений элементарных площадок на квадраты их расстояний до полюса:

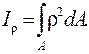(4.6)

Осевые и полярный моменты инерции являются величинами существенно положительными. Пользуясь рис. 4.1, установим связь между полярным и осевым моментами инерции сечения:

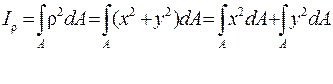
Окончательно, учитывая формулы (4.5), имеем:

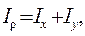(4.7)

т.е. полярный момент инерции равен сумме осевых моментов инерции относительно любой пары взаимно перпендикулярных осей, проходящих через полюс.

Центробежным моментом инерции сечения относительно некоторых двух взаимно перпендикулярных осей называется взятая по всей его площади сумма произведений элементарных площадок на их расстояния до этих осей:

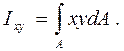(4.8)

В зависимости от расположения осей центробежный момент инерции может быть положительным, отрицательным и равным нулю.

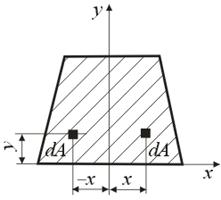Рассмотрим центробежный момент инерции сечения относительно осей, одна из которых является осью симметрии фигуры (рис. 4.3). Легко заметить, что для каждой положительной величины 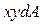в первом квадранте можно найти такую же отрицательную во втором квадранте, т. е. для всей фигуры

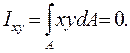
Итак, если хотя бы одна из осей является осью симметрии фигуры, то центробежный момент инерции сечения относительно этой оси и любой ей перпендикулярной равен нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными. Если начало координат этих осей совпадает с Рис 4.3 центром тяжести сечения, то их называют главными центральными.

Из определения моментов инерции (4.5), (4.8) очевидно, что они характеризуют расположение сечения относительно осей. Размерность моментов инерции – (ед. длины)⁴, например, мм⁴, см⁴, м⁴.

МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ СЕЧЕНИЙ

Прямоугольник (рис. 4.4)

Вычислим моменты инерции относительно главных центральных осе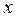й и 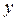. Для определения момента инерции относительно оси, выделим элементарную площадку в виде узкого прямоугольника, параллельного оси :

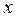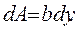
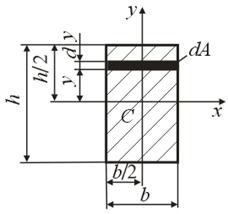
Рис.4.4

Момент инерции находим по формуле (4.5):

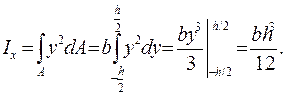(4.9)

Очевидно, что относительно другой главной центральной оси 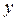момент инерции определяется как

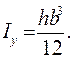(4.10)

Треугольник (рис.4.5)

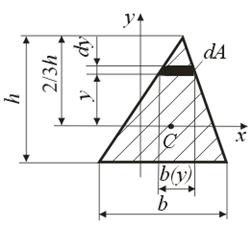Найдем момент инерции относительно центральной оси 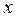. Выделим элементарную площадку в виде полоски, параллельной оси :

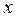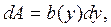
где .

Рис.4.5

В соответствии с формулой (4.5) получим:

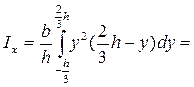
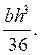(4.11)

Круг (рис.4.6)

Вычислим полярный момент инерции круга относительно его центра. Для этого радиусами и 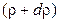выделим произвольно расположенное бесконечно тонкое кольцо, площадь которого найдем как площадь прямоугольника со сторонами и :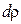

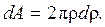
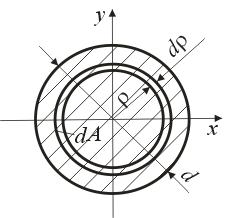
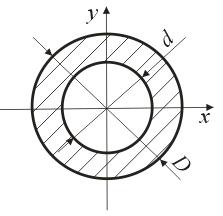
Рис.4.6 Рис. 4.7

Полярный момент инерции круга

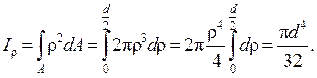(4.12)

Моменты инерции круга относительно центральных осей легко найти на основании зависимости (4.7). В силу симметрии

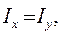
следовательно

(4.13)

Кольцо (рис.4.7)

Моменты инерции кругового кольца определяются точно так же, как круга, но с учетом изменения нижнего предела интегрирования в связи с наличием отверстия:

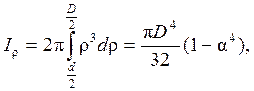(4.14)

где 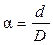- коэффициент ослабления сечения, величина которого зависит от размера отверстия.

На основании соотношения (4.7) может быть получена формула для осевого момента инерции кольца:

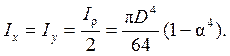(4.15)

МОМЕНТЫ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ

При вычислении моментов инерции сложных сечений последние разбивают на отдельные простые составляющие фигуры, моменты инерции которых известны. Из основного свойства интеграла следует, что момент инерции сложной фигуры равен сумме моментов инерции составляющих ее частей.

Найдем момент инерции сложного сечения относительно оси 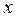(см. рис.4.2). Разобьем сечение на простые фигуры. При вычислении будем последовательно суммировать произведения 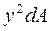, охватывая площади 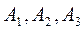простых фигур. Тогда

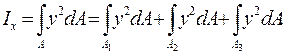
Очевидно, каждый из интегралов правой части представляет собой момент инерции соответствующей простой фигуры: 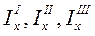, т.е.

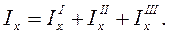
Таким образом, для сложных сечений моменты инерции связаны следующими соотношениями:

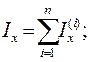
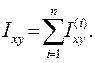(4.16)

Заметим, что отверстие в сечении следует считать фигурой с отрицательной площадью.

ЗАВИСИМОСТЬ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ КООРДИНАТ

Пусть известны моменты инерции произвольного сечения относительно взаимно перпендикулярных осей 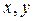(рис.4.8, а), которые определены согласно формулам (4.5) и (4.8):

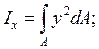
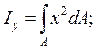
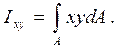
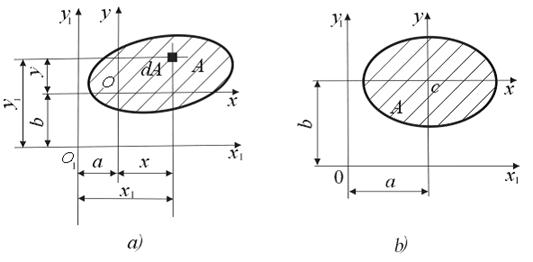
Рис. 4.8

Найдем моменты инерции относительно осей , которые параллельны заданным осям :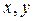

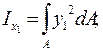
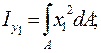
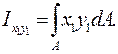
Координаты любой точки в новой системе x ₁ ,y ₁ могут быть выражены через координаты в осях :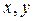

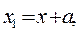
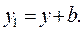
где 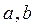- координаты старого начала координат осей 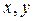в новой системе . Подставляя значение 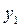в выражение для 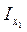, имеем

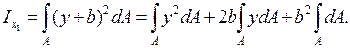
Учитывая, что

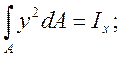
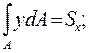
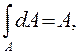
окончательно получаем

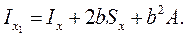(4.17)

Аналогично может быть найдено выражение для момента инерции относительно оси :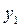

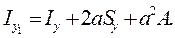(4.18)

Центробежный момент инерции относительно осей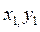

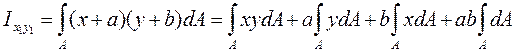
или

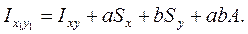(4.19)

Если исходные оси являются центральными (см. рис.4.8, б), то формулы при параллельном переносе осей упрощаются, так как статические моменты 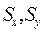обращаются в нуль:

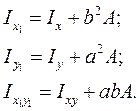(4.20)

Отметим, что в последнюю из этих формул координаты 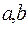следует подставлять с учетом их знака (в системе координат ).

Следует подчеркнуть, что относительно любой нецентральной оси осевые моменты инерции больше, чем относительно параллельной ей центральной.

ЗАВИСИМОСТЬ МЕЖДУ МОМЕНАМИ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ КООРДИНАТ

Будем считать известными моменты инерции сечения 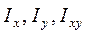. Определим моменты инерции 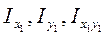относительно осей (рис.4.9), повернутых на угол α (напомним, что в правой системе координат α>0 при повороте против хода часовой стрелки).

Установим связь между координатами и :

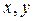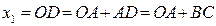или .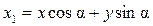

Аналогично найдем : .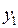

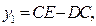
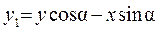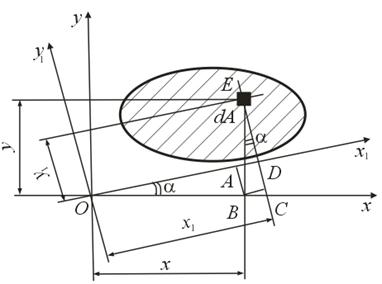
Рис.4.9

По определению 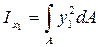, после подстановки 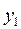имеем

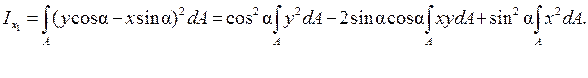Учитывая, что

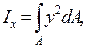
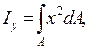
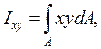
получаем

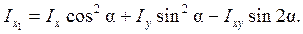
Используя известные тригонометрические соотношения

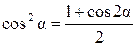и ,

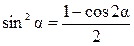приведем выражение к окончательному виду:

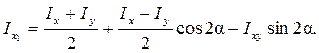(4.21)

Путем аналогичных преобразований получим выражение для 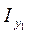и :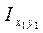

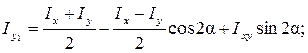(4.22)

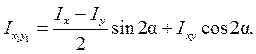(4.23)

Складывая почленно выражения (4.21) и (4.22),получаем

,

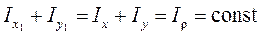т. е. при повороте осей сумма осевых моментов инерции не изменяется. Следовательно, если один момент инерции возрастает, то другой убывает; один достигает максимального значения, другой – минимального.

Исследуем функцию (4.21) на экстремум, чтобы установить оси, относительно которых осевые моменты инерции сечения экстремальны:

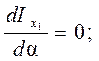
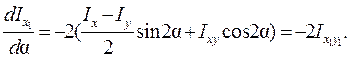
Таким образом, условием экстремальности осевых моментов инерции является равенство нулю центробежного момента инерции относительно этих осей, т. е. осевые моменты инерции имеют максимальное и минимальное значения относительно главных осей, которым в случае несимметричных сечений дают свои обозначения, например, u и v.

Рассмотрим частный случай задачи, в которой известны моменты инерции относительно главных осей 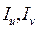(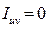), а требуется определить осевые и центробежные моменты инерции сечения относительно осей 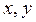, повернутых от главных осей u, v на угол 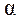. Нужные формулы легко получить из соотношений (4.21), (4.22), (4.23):

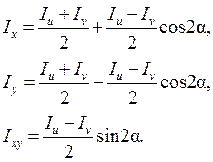(4.24)

ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЯ ГЛАВНЫХ ОСЕЙ. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

По определению центробежный момент инерции относительно главных осей u и v равен нулю, т.е. I_uv =0. Приравнивая нулю правую часть выражения (4.23) при 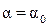, получим

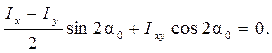Это уравнение дает формулу для нахождения угла 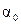, определяющего положение главных осей u, v несимметричного сечения (см. рис.4.10), для которого известны моменты инерции I_x, I_y и I_xy:

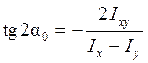
или

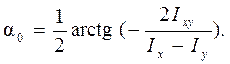(4.25)

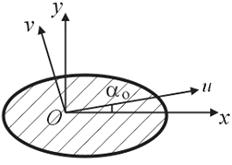
Рис.4.10

Положительное значение угла 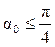откладываем от оси против хода часовой стрелки и получаем положение главной оси u, ось v перпендикулярна ей. Если 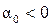, то откладываем его по ходу часовой стрелки. Это правило знаков справедливо для правой системы координатных осей. Если расчеты моментов инерции выполняются в левой системе координат, то правило знаков для угла 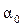изменяется на обратное.

Для вычисления главных моментов инерции следует подставить в формулы (4.21) и (4.22) значение :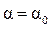

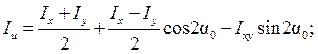(4.26)

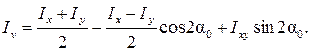(4.27)

Можно также получить формулы для вычисления главных моментов инерции, не содержащие тригонометрических функций. Для этого используем формулы (4.26), (4.27) и представление (4.23) для центробежного момента инерции относительно главных осей u,v ():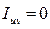

.

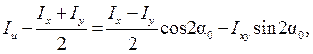
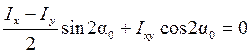Возведем в квадрат правые и левые части этих выражений, сложим их и после простых преобразований получим весьма удобную для практических расчетов формулу:

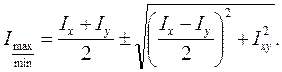(4.28)

Сумма дает значение наибольшего главного момента инерции 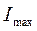, разность – наименьшего .

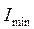Для ответа на вопрос, относительно какой из осе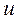й (или 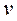) момент инерции максимален, надо руководствоваться следующим правилом: если 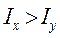, то 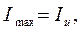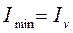; если 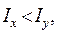то 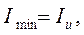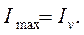В большинстве случаев правильный ответ может быть дан, исходя из формы сечения и его расположения относительно главных осей.

ПОНЯТИЕ О РАДИУСЕ ИНЕРЦИИ СЕЧЕНИЯ

Момент инерции сечения относительно какой-либо оси на основании известной из курса математического анализа теоремы о среднем можно представить в виде произведения площади всего сечения на квадрат некоторого отрезка, называемого радиусом инерции сечения, например:

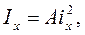
где 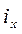- радиус инерции относительно оси .

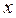На основании приведенного определения радиусы инерции сечения относительно осей x и y могут быть выражены как

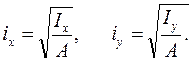(4.29)

Главным центральным осям инерции соответствуют главные радиусы инерции:

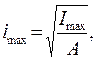
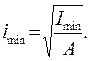(4.30)

Например, для прямоугольника, изображенного на рис.4.4, главные радиусы инерции

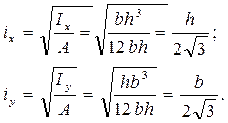
Размерность радиуса инерции-(ед.длины), например, мм, см, м.

Радиусы инерции сечения являются еще более явственной характеристикой формы сечения, чем моменты инерции, так как в них исключено влияние площади. В практических расчетах обычно применение находят главные радиусы инерции.

МОМЕНТЫ СОПРОТИВЛЕНИЯ СЕЧЕНИЯ

Полярным моментом сопротивления сечения называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения:

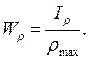(4.31)

Осевым моментом сопротивления сечения называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки сечения:

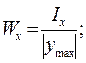
(4.32)

Практический интерес представляют моменты сопротивления относительно главных осей, являющихся осями симметрии. Размерность момента сопротивления-(ед. длины)³, например, мм³, см³, м³.

Найдем моменты сопротивления для некоторых фигур.

Прямоугольник

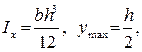следовательно

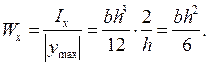
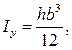
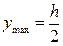, следовательно

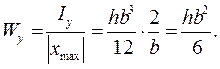
Круг

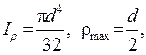следовательно

.

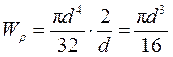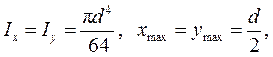следовательно

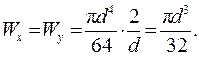
Кольцо

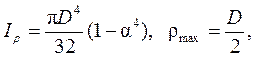следовательно

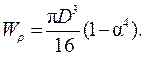
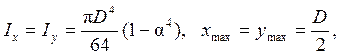следовательно

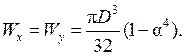
Полярные моменты сопротивления используются в расчетах на прочность при кручении, осевые – при изгибе. Заметим, что при вычислении моментов сопротивления сложных сечений их нельзя ни складывать, ни вычитать, так как моменты сопротивления не являются интегральными величинами (как статические моменты или моменты инерции); в таких случаях расчет выполняется в соответствии с формулами (4.31) и (4.32).

Дата добавления: 2014-01-06