Лекция 6

СДВИГ

Лекция 5

РАСЧЕТ НА СРЕЗ

С деформацией сдвига мы встречаемся, когда из шести внутренних силовых факторов отлична от нуля только поперечная сила Q_y (или Q_x). С достаточной степенью приближения деформация сдвига или среза практически может быть получена в случае, когда на стержень с противоположных сторон на весьма близком расстоянии друг от друга действуют две равные силы, перпендикулярные к его оси и направленные в противоположные стороны. Примером может служить резка ножницами полосы, прутьев и т.п. (рис. 5.1, а,б).

Получим формулу для напряжений в поперечном сечении стержня, представленного на рис. 5.1. Пусть известна внешняя нагрузка F. Используя метод сечений, находим, что на участке bc поперечная сила

Q_y = F.

Опуская в дальнейшем индекс при Q, запишем интегральную связь (1.1) между поперечной силой и напряжениями, действующими в рассмотренном сечении, в следующем виде:

. (5.1)

Принимая касательные напряжения τ равномерно распределёнными по площади поперечного сечения F (рис. 5.2), на основании выражения (5.1) имеем

,

откуда

. (5.2)

Рис. 5.1

Рис. 5.2

Допущение о равномерности касательных напряжений по сечению весьма условно, однако оно широко используется в инженерной практике при расчёте болтов, шпонок, заклёпочных и сварных соединений и других деталей.

Условие прочности на сдвиг (срез) по методу предельных состояний записывается в виде

, (5.3)

где R _ср – расчётное сопротивление материала на срез, величина которого зависит от свойств материала. Отметим, что для пластичных материалов

.

ПОНЯТИЕ О ЧИСТОМ СДВИГЕ

Выделим из бруса, представленного на рис. 5.2, элементарный параллелепипед (элемент) в окрестности данной точки поперечного сечения (рис. 5.3, а).

Компоненту касательных напряжений, возникающих на боковых гранях элемента (в поперечных сечениях), обозначим τ _zy. Очевидно, что для равновесия элемента на горизонтальных гранях (в продольных сечениях) должны быть указаны компоненты напряжений τ_yz. Найдём соотношение этих напряжений из условия равновесия элемента в виде:

.

Сократив это выражение на произведение dxdydz, получим равенство

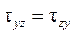, (5.4)

называемое законом парности касательных напряжений: на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные общему ребру, равны по величине и направлены в противоположные стороны.

Рис. 5.3

Таким образом, в плоскости на гранях прямоугольного элемента действуют касательные напряжения 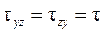(см. рис. 5.3, б).

Напряжённое состояние, при котором на гранях выделенного элемента действуют только касательные напряжения, называют чистым сдвигом.

Типичным примером тела, во всех точках которого имеет место чистый сдвиг, является скручиваемая тонкостенная труба, показанная на рис.5.4, а. Прямоугольные до деформации элементы материала стенок трубы превращаются в параллелограммы за счёт изменения первоначально прямого угла на малый угол g (рис.5.4, б).

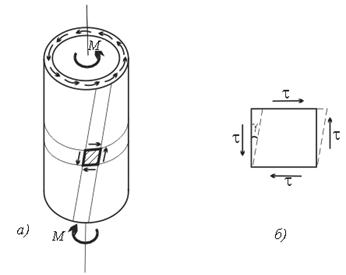
Рис. 5.4

ЗАКОН ГУКА ПРИ ЧИСТОМ СДВИГЕ

Рассмотрим деформацию элемента, ограниченного площадками чистого сдвига. Для наглядности закрепим его по одной из граней (рис. 5.5). Под действием касательных напряжений верхняя грань сдвигается параллельно нижней, превращая прямоугольный элемент в параллелограмм. При этом высота элемента остаётся неизменной, а первоначально прямые углы изменяются на малый угол g, называемый углом сдвига или относительным сдвигом.

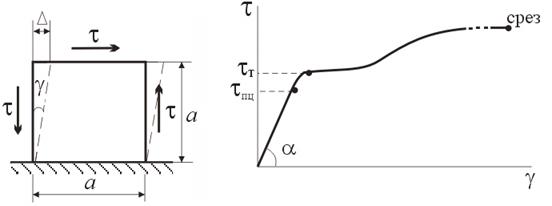
Рис.5.5 Рис.5.6

Величину смещения грани обозначают ∆ и называют абсолютным сдвигом.

Выражая угол в радианах, и учитывая его малость, можно принять , тогда относительный сдвиг выразится следующим образом

(5.5)

Экспериментальное изучение деформации чистого сдвига обычно проводят путём кручения трубчатых образцов, получая зависимость между напряжением 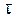и углом сдвига 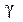. Типичный вид диаграммы сдвига для пластичной стали показан на рис.5.6. До предела пропорциональности при сдвиге τ_пц справедлива линейная зависимость

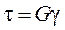, (5.6)

называемая законом Гука при сдвиге. Здесь G – коэффициент пропорциональности, который называется модулем сдвига материала или модулем упругости II рода. Из выражения (5.6) следует, что модуль G имеет размерность напряжений (Па), так как g - величина безразмерная. Можно показать, что модуль сдвига не является независимой константой материала и может быть определен для изотропного материала через модуль упругости E и коэффициент Пуассона μ с помощью соотношения

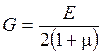. (5.7)

Например, для стали E = 2×10⁵ МПа, μ = 0,25, откуда следует, что G =0,8×10⁵ МПа. Зависимость (5.7) подтверждается экспериментально.

Напряжение τ_т является пределом текучести при сдвиге, т.е. касательным напряжением, при котором угол сдвига возрастает при постоянном напряжении. Характерно, что для многих материалов предел текучести при сдвиге τ_т связан с пределом текучести при растяжении σ_т соотношением

.

Запишем выражение для абсолютного сдвига ∆, подставив в формулу закона Гука (5.6) полученные ранее соотношения (5.2) и (5.5):

,

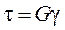или

,

откуда

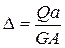, (5.8)

где произведение GA называют жесткостью сечения при сдвиге.

ПРАКТИЧЕСКИЕ РАСЧЕТЫ СОЕДИНЕНИЙ, РАБОТАЮЩИХ НА СДВИГ

Детали, служащие для соединений отдельных элементов машин и строительных конструкций, - заклёпки, штифты, болты и т.п. – во многих случаях воспринимают нагрузки, перпендикулярные к их продольной оси. Поперечная нагрузка в указанных деталях возникает, в частности, при растяжении (сжатии) соединяемых элементах. Соответствующие примеры приведены на рис. 5.8, где изображены а – штифт, б – заклёпка, в – болт, поставленный без зазора, г – шпонка. Их действительная работа сложна и лишь приближенно может быть охарактеризована как работа на сдвиг (срез). Однако практические расчёты этих соединений очень просты и достаточно надёжны, так как расчётные сопротивления назначаются на основании опытных данных.

Рис. 5.7

Расчеты деталей на срез базируются на следующих основных допущениях:

1) в поперечном сечении возникает только один внутренний силовой фактор– поперечная сила Q;

2) касательные напряжения распределены равномерно по площади поперечного сечения;

3) в случае, если соединение осуществлено несколькими одинаковыми деталями (заклепками и т. п.), принимается, что все они нагружены одинаково.

Разрушение соединительных элементов (в случае недостаточной прочности) происходит в результате их перерезывания по плоскости, совпадающей с поверхностью соприкосновения соединяемых деталей, как показано на рис.5.8, поэтому говорят, что эти элементы работают на срез, и возникающие в их поперечном сечении касательные напряжения называют напряжениями среза и обозначают τ_ср.

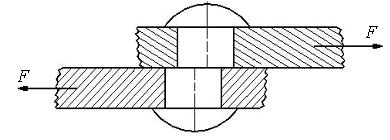
Рис. 5.8

Условие прочности на срез формулируется как

, (5.9)

где Q – поперечная сила; при нескольких одинаковых соединительных деталях ; здесь F – общая нагрузка соединения, п – число заклёпок (болтов и т.п.); R _ср – расчётное сопротивление материала соединительных элементов.

Формула (5.9) используется для проверочного расчёта соединения. В зависимости от постановки задачи она может быть преобразована для определения допускаемой (расчётной) нагрузки или требуемой площади сечения.

Расчёт на срез обеспечивает прочность соединительных элементов, но не гарантирует надёжность соединения в целом. При недостаточной толщине соединяемых элементов возможно нарушение соединения вследствие их смятия по поверхности контакта с соединительными деталями. Давления, возникающие между поверхностями отверстий и соединительных деталей, принято называть напряжениями смятия и обозначать σ_см. Фактическое распределение контактных напряжений весьма сложно. Поэтому расчёт на смятие носит условный характер и ведётся в предположении, что силы взаимодействия между деталями равномерно распределены по поверхности контакта и нормальны к этой поверхности.

Условие прочности на смятие имеет вид

, (5.10)

где 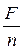- нагрузка на одну соединительную деталь; A _см – расчётная площадь смятия; R _см – расчётное сопротивление на смятие, определяемое экспериментально.

За расчётную площадь смятия при контакте по плоскости (см. рис. 5.7, г) принимают действительную площадь соприкосновения – A _см = tl, где l – размер шпонки в направлении, перпендикулярном плоскости чертежа; при контакте по цилиндрической поверхности (см. рис.5.7, а,б,в) принимают площадь проекции поверхности контакта на диаметральную плоскость, т.е. A _см = d. При различной толщине соединяемых элементов в расчётную формулу следует подставлять 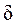_min.

Для примера рассмотрим некоторые вопросы расчета заклёпочных соединений для случаев, когда соединяемые элементы работают на растяжение и сжатие.

На рис. 5.9, а показана работа одиночной заклёпки, соединяющей три листа и называемой двухсрезной, так как при её разрушении срез происходит по двум сечениям(отмечено волнистой линией) с площадью среза .

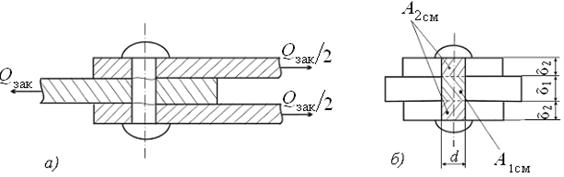
Рис. 5.9

Зависимости для проверочных расчётов имеют следующий вид:

а) на срез

, (5.11)

где п – общее число заклёпок, передающих заданную нагрузку F;

k – число плоскостей среза одной заклёпки;

d – диаметр заклёпки;

б) на смятие

, (5.12)

где – наименьшая суммарная толщина листов, сминаемых в одном направлении. Например, на рис.5.9, б это будет меньшая из площадей A _{1с м} = = d и A_{2 см} = 2 d.

Допускаемую силу на одну заклёпку определяют следующим образом:

а) из условия прочности на срез

; (5.13)

б) из условия прочности на смятие

. (5.14)

Из двух сил фактической допускаемой силой для заклёпки Q _зак является меньшая из них.

Расчёт заклёпочного соединения обычно состоит в определении необходимого числа заклёпок п при действии на него заданной нагрузки F. Тогда

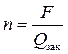. (5.15)

Дата добавления: 2014-01-06