Для схем 7.1,а,г опорные реакции проще найти из уравнений

å m_A = 0; å F_y = 0,

(для схемы 7.1, г, дополненных уравнением åm_В = 0 для левой или правой частей балки), а проверить с помощью уравнения

åm_c = 0.

Отметим, что наложенные на балку связи должны обеспечивать кинематическую неизменяемость системы – невозможность её перемещения как твёрдого тела.

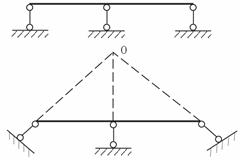
Рис.7.2

На рис. 7.2 показаны случаи, когда это требование не выполняется: линии действия связей параллельны, либо пересекаются в одной точке. Здесь мы имеем дело с механизмами, в которых перемещения возможны без деформации конструкции, несмотря на то, что число связей равно трём, т.е. совпадает с количеством независимых уравнений равновесия. На практике часто встречаются системы, в которых число наложенных связей больше числа независимых уравнений равновесия, например, балки с дополнительными опорами. Такие системы называют статически неопределимыми, поскольку опорные реакции в них не могут быть определены только из уравнений равновесия.

С методами расчёта статически неопределимых систем мы встретимся позже.

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ ИЗГИБЕ БАЛОК.

ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ

Как мы ранее условились, внешние силы действуют в плоскости симметрии балки yOz перпендикулярно её оси. В поперечных сечениях балки при этом возникают лишь два внутренних силовых фактора – изгибающий момент М_x и поперечная сила Q_y. Для их нахождения используют метод сечений – балка мысленно рассекается плоскостью, перпендикулярной оси, одна из частей отбрасывается, а действие отброшенной части на оставшуюся заменяется внутренними усилиями, как это показано на рис. 7.3.

Здесь О - центр тяжести сечения п-п. Величина внутренних усилий находится из условий равновесия оставшейся части:

åF_y = 0: Q_y = R_A - F;

åm₀ = 0: M_x = R_A×z – F(z – a) (7.1)

Поперечная сила в сечении численно равна алгебраической сумме внешних сил, приложенных к оставшейся части балки; изгибающий момент - алгебраической сумме этих же сил относительно горизонтальной оси x, проходящей через центр тяжести сечения.

Введем следующие правила знаков:

1) поперечная сила положительна, если направлена так, что стремится повернуть оставшуюся часть балки по ходу часовой стрелки;

2) изгибающий момент положителен, если он стремиться изогнуть балку выпуклостью вниз, вызывая растяжения нижних волокон.

На рис. 7.4 показаны положительные направления внутренних усилий

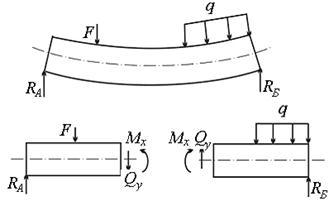
Рис. 7.4

Чтобы легче запомнить эти правила и не ошибиться в выборе знака слагаемых в правой части уравнений вида (7.1), отметим следующее (рис. 7.5):

а) правило знаков для поперечной силы по сути является исключением для правил, связанных с поворотом - за положительное обычно принимают направление против хода часовой стрелки;

б) правило знаков для изгибающего момента с ходом часовой стрелки никак не связано. Чтобы запомнить его, достаточно взглянуть на рожицы рис. 7.5, где знак эмоций совпадает со знаком момента.

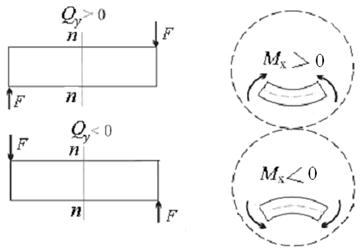
Рис.7.5

Между внутренними силовыми факторами при изгибе и внешней распределённой нагрузкой существуют важные дифференциальные зависимости.

Рассмотрим балку, нагруженную распределёнными по её длине вертикальными силами, интенсивность которых q (z) может быть переменной (рис. 7.6)

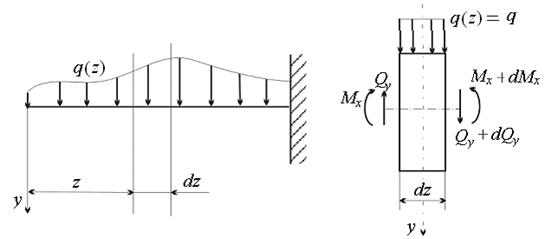
Рис. 7.6

Поскольку большая часть нагрузок в строительстве связана с весом, удобнее направить ось y вниз и считать нагрузку такого направления положительной. С помощью двух бесконечно близких поперечных сечений выделим из балки элемент длиной dz. Действие на элемент левой отброшенной части балки заменим поперечной силой Q_y и изгибающим моментом М_x, действие правой – поперечной силой Q_y + dQ_y и моментом M_x + dM_x. Приращение внутренних усилий dQ_y и dM_x вызваны приращением координаты dz. Ввиду малости элемента, действующую на него распределённую нагрузку можно считать равномерной: q (z) = q = const.

Для того, чтобы выделенный элемент находился в равновесии, должны выполняться следующие условия:

åF_y = 0:

åm₀ = 0: 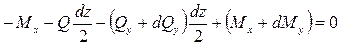(7.2)

Дата добавления: 2014-01-06