В точке тела

ЭЛЕМЕНТЫ ТЕОРИИ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ

Лекция 16

Как было сказано ранее, деформированным состоянием в точке тела называют совокупность деформаций по различным осям и в различных плоскостях, проходящих через данную точку, а сами деформации 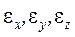, называют компонентами деформированного состояния.

Линейные деформации 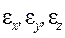связаны законом Гука с нормальными напряжениями на гранях элемента, а угловые деформации зависят только от касательных напряжений. Подобно тому, как для описания напряженного состояния в точке тела был использован тензор напряжений , для деформированного состояния введем тензор деформаций

.

Между компонентами тензоров Т _σ и Т _ε существует прямая математическая аналогия, поэтому все формулы, полученные при анализе напряженного состояния, остаются справедливыми при замене нормальных напряжений на линейные деформации: а касательных напряжений – на половину соответствующих величин угловых деформаций:

.

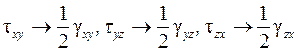Главным напряжениям 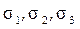соответствуют главные линейные деформации . При этом главные направления обоих тензоров для упругого изотропного тела совпадают, главные деформации экстремальны, а угловые деформации на главных площадках равны нулю.

ОБОБЩЁННЫЙ ЗАКОН ГУКА

При рассмотрении растяжения и сжатия мы выяснили, что линейная деформация в продольном направлении связана с напряжением в поперечном сечении стержня законом Гука:

.

При этом в поперечном направлении возникает деформация, которая определяется через продольную деформацию с помощью коэффициента Пуассона:

.

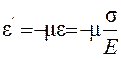Для того чтобы обобщить ранее полученный результат на случай объёмного напряженного состояния, рассмотрим деформацию элементарного параллелепипеда размерами . Ориентацию элемента выберем такой, чтобы по его граням действовали главные напряжения 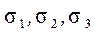, то есть координатные оси совпадали с главными направлениями (рис. 16.1).

Рис. 16.1

Вследствие деформации, длины рёбер изменятся и станут равными . Относительные удлинения ребер параллелепипеда представляют собой главные деформации:

(16.1)

На основании принципа суперпозиции можно записать:

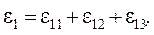
где 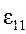- линейная деформация в направлении первого главного напряжения, вызванного действием только σ₁;

- линейная деформация в том же направлении, вызванная действием главного напряжения σ₂;

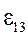- линейная деформация в том же направлении от действия напряжения σ₃.

Направление для самого напряжения является продольным, а для напряжений и 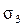- поперечным, поэтому

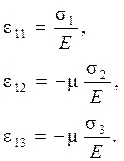
Сложив эти величины, получим

Проделав аналогичные выводы для двух других главных направлений, получим

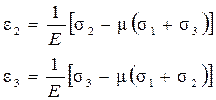(16.2)

Выражения (16.2) представляют собой обобщенный закон Гука для главных деформаций. Поскольку деформации принимаются малыми, влиянием сдвигов на линейные деформации можно пренебречь, и считать формулы (16.2) справедливыми не только для главных деформаций, но и для линейных деформаций по любым трем взаимно перпендикулярным направлениям. В этом случае обобщенный закон Гука необходимо дополнить выражениями для угловых деформаций:

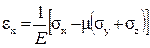
(16.3)

Отметим, что для плоского напряженного состояния, например для случая 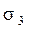=0, из (16.2) будем иметь

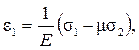
Как видим, деформированное состояние при этом не является плоским.

ОБЪЁМНАЯ ДЕФОРМАЦИЯ

Найдем относительное изменение объёма элементарного параллелепипеда, показанного на рис.16.1. До деформации элемент занимал объём 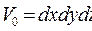. Его объём после деформации

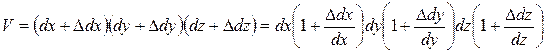
Учитывая (16.1), абсолютное изменение объёма можно представить в виде

Учитывая малость деформаций, их произведениями можно пренебречь, тогда получим

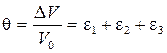(16.4)

Величину 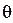называют объёмной деформацией или относительным изменением объёма. Подставив в формулу (16.4) выражения деформаций из обобщенного закона Гука (16.2), будем иметь

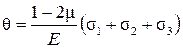(16.5)

Если ввести понятие среднего напряжения

,

то можно получить ещё одну форму записи закона Гука:

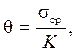(16.6)

где 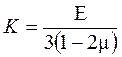- модуль объёмной упругости.

Из (16.6) следует, что при значении коэффициента Пуассона , объём тела при нагружении не изменяется. Примерами таких несжимаемых материалов могут служить резина и парафин, а также сталь в состоянии температурной текучести.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ

Потенциальной энергией деформации называют энергию, которая накапливается в теле при его статическом упругом деформировании. Поскольку при таком нагружении кинетическая энергия системы не меняется, а потери энергии в упругих материалах невелики, можно считать потенциальную энергию деформации численно равной работе внешних сил, совершённой ими при деформации тела.

Рассмотрим стержень с начальным поперечным сечением A и длиной l, растягиваемый медленно возрастающей силой F (рис. 16.2).

Рис.16.2

Если материал стержня подчиняется закону Гука, то зависимость нагрузки от удлинения линейна. Элементарная работа при изменении силы на величину dF, а удлинения – на величину d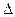l, равна произведению Fd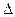l, что соответствует на рис. 16.2 площади заштрихованной фигуры. Полная работа, совершаемая в процессе нагружения, представляет собой интегральную сумму таких элементарных площадей и равна площади треугольника, образованного диаграммой растяжения и горизонтальной осью:

W = U =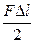 (16.7)

Здесь W - работа внешней силы F на удлинении стержня 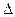l;

U - потенциальная энергия упругой деформации стержня.

Введём понятие удельной энергии деформации, разделив полную энергию U на объём стержня:

u =,

где – нормальное напряжение в поперечном сечении стержня,

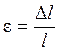- соответствующая линейная деформация.

Обобщая полученный результат на случай объемного напряженного состояния, когда одновременно действуют все три главные напряжения, получим:

u = (16.8)

Можно воспользоваться обобщенным законом Гука (16.2) и выразить удельную потенциальную энергию деформации через главные напряжения:

u = 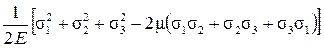(16.9)

В общем случае нагружения выделенный из тела элементарный параллелепипед в процессе деформации меняет как свою форму, так и свой объем. Выделим ту часть удельной потенциальной энергии, которая связана с изменением формы. Для этого представим, напряженное состояние в элементе в виде суперпозиции двух состояний, как это показано на рис.16.3. В первом состоянии (состояние I) на гранях элемента действуют введенные ранее средние напряжения , а во втором (состояние II) – напряжения, дополняющие первое состояние до исходного. Первое напряженное состояние представляет собой всестороннее растяжение, либо всестороннее сжатие в зависимости от знака среднего напряжения, т.е. приводит лишь к изменению объема элемента, без искажения его формы.

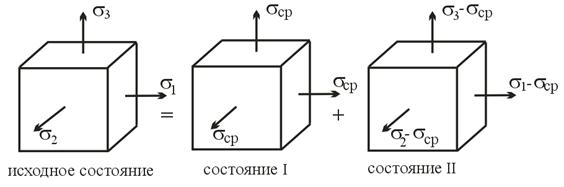
Рис.16.3.

Следовательно, второе состояние связано именно с изменением формы элемента и не должно приводить к изменению объема. Чтобы убедиться в этом, вычислим объемную деформацию в состояниях I и II:

;

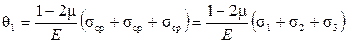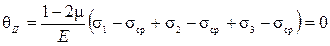
Как видим, относительное изменение объема в первом и в исходном напряженном состояниях совпадают. В состоянии II изменение объема не происходит, значит, вся потенциальная энергия деформации этого состояния идет на изменение формы элемента.

Будем называть удельную потенциальную энергию деформации, накапливаемую в состоянии I, энергией изменения объема u_V, а в состоянии II – энергией формоизменения u _Ф:

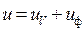
Удельную потенциальную энергию изменения объема легко вычислить, подставив в формулу (16.9) вместо главных напряжений среднее напряжение:

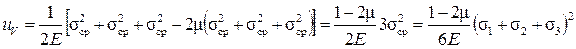
Удельную потенциальную энергию формоизменения проще найти как разность удельной потенциальной энергии u и найденного выражения u_V:

После несложных преобразований окончательно получаем:

(16.10)

Найденное выражение понадобится нам далее при записи формулировки одной из самых часто применяемых теорий прочности.

Дата добавления: 2014-01-06