Теории прочности

Лекция 17

Одной из главных задач инженерного расчёта является оценка прочности конструкции по известному напряжённому состоянию. В случае простых видов нагружения опасные напряжения, при которых конструкция переходит в предельное состояние, легко находятся экспериментально. Так, если напряжённое состояние в элементе конструкции является одноосным, переход в предельное состояние происходит тогда, когда нормальное напряжение достигает предела текучести в пластичном материале или предела прочности в хрупком. В случае плоского или объёмного напряжённого состояния ситуация существенно усложняется. Очевидный на первый взгляд путь экспериментального исследования прочности образцов при соответствующем нагружении приходится отклонить. Это объясняется как неоправданным усложнением испытательного оборудования, так и необходимостью проведения бесчисленного множества экспериментов, поскольку для каждой новой комбинации нормальных и касательных напряжений испытания пришлось бы проводить заново. В связи с этим представляется заманчивым найти такой критерий прочности, при достижении которого сложное напряжённое состояние становится предельным. Существуют различные теории о преимущественном влиянии на прочность того или иного фактора, который и принимается в качестве соответствующего критерия прочности. Все они используют понятие равнопрочности, которое можно сформулировать следующим образом: два различных напряжённых состояния считаются равнопрочными (равноопасными), если при пропорциональном увеличении их главных напряжений в одно и то же число раз, они одновременно становятся предельными. Число, на которое умножаются главные напряжения для перехода в предельное состояние, представляет собой ничто иное, как коэффициент запаса прочности.

Предельное значение фактора, определяющего прочность, легко находится на основании стандартных опытов на растяжение и сжатие. Критерий прочности позволяет сопоставить исследуемое сложное напряжённое состояние с простым, например осевым растяжением, и установить эквивалентное (равноопасное) напряжение в растянутом стержне с таким же коэффициентом запаса (рис.17.1).

Приравняв друг другу выражения выбранного по соответствующей теории критерия прочности для этих напряжённых состояний, можно получить зависимость вида

σ_э = f ( σ₁, σ₂, σ₃ ) = σ_оп,

которая описывает условие наступления предельного состояния. В качестве опасного напряжения σ_оп для пластичных материалов берётся предел текучести σ_т, для хрупких – предел прочности σ_в.

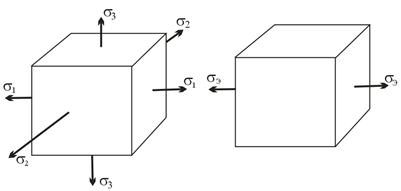
Рис. 17.1

В соответствии с методом предельных состояний условие прочности при сложном напряжённом состоянии в общем случае можно сформулировать следующим образом

σ_э = f ( σ₁, σ₂, σ₃ ) ≤ R. (17.2)

Здесь R – расчётное сопротивление материала.

Различные теории прочности приводят к различным выражениям для эквивалентного напряжения. Наличие нескольких теорий не должно вызывать удивления, поскольку каждый из критериев прочности

(наибольшее нормальное напряжение, наибольшая линейная деформация, потенциальная энергия деформации и т.д.) лишь отчасти отражает весьма сложный процесс наступления предельного состояния и применим только в определённых условиях. Далее мы познакомимся с наиболее простыми, классическими теориями прочности.

I. ТЕОРИЯ НАИБОЛЬШИХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ

(первая теория прочности)

Преимущественное влияние на прочность по этой теории оказывает величина наибольшего нормального напряжения. Считая эквивалентное напряжение равным наибольшему главному напряжению, условие наступления предельного состояния можно записать в виде

σ_э = σ₁ = σ_оп,

где σ_оп – опасное напряжение, принимаемое равным σ_т или σ_в.

Условие прочности по методу предельных состояний примет вид

σ_э = σ₁ ≤ R, (17.3)

где R – расчётное сопротивление материала. Эта теория не получила экспериментального подтверждения, и в настоящее время представляет лишь исторический интерес.

II. ТЕОРИЯ НАИБОЛЬШИХ ЛИНЕЙНЫХ ДЕФОРМАЦИЙ

(вторая теория прочности)

В качестве критерия прочности по этой теории выступает величина наибольшего линейного удлинения ε₁. Условие наступления предельного состояния имеет вид

,

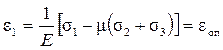где ε_оп = σ_оп / Е – предельное значение относительного удлинения, которое находится из опыта на растяжение. Отсюда следует условие для эквивалентного напряжения, обеспечивающее прочность элемента конструкции:

σ_э = σ₁ – μ (σ₂ + σ₃) ≤ R (17.4)

Для плоского напряжённого состояния одно из главных напряжений обратится в нуль, а два оставшихся можно выразить через напряжения на произвольных площадках по формулам (15.6).

Условие прочности при этом записывается следующим образом

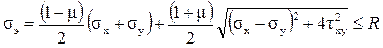(17.5)

Теория наибольших линейных деформаций предполагает, что материал подчиняется закону Гука вплоть до момента разрушения. По этой причине данная теория даёт удовлетворительное совпадение с экспериментом только для очень хрупких материалов, разрушающихся без заметных остаточных деформаций. При этом следует иметь в виду, что условия (17.4) и (17.5) применимы лишь в тех случаях, когда величина σ_э оказывается положительной. Таким образом, вторая теория прочности в отличие от первой, иногда используется и в настоящее время, но лишь для хрупких материалов и в определённых условиях нагружения.

III. ТЕОРИЯ НАИБОЛЬШИХ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ

(критерий пластичности Треска – Сен-Венана)

Многочисленные эксперименты говорят о том, что механизм образования пластичных деформаций тесно связан со сдвигами в материале, а те, в свою очередь, зависят от величины касательных напряжений.

Сен-Венаном в качестве критерия перехода материала в пластическое состояние было предложено использовать величину наибольших касательных напряжений τ_max. В случае объёмного напряжённого состояния

.

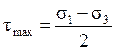Появление необратимых деформаций происходит при нарушении условия

τ_max < τ_оп ,

где τ_оп = σ_оп / 2 – находится из опыта на простое растяжение, в качестве опасного напряжения σ_оп принимается предел текучести σ_т. Условие прочности по данной теории можно записать в следующем виде

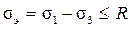, (17.6)

где R – расчётное сопротивление материала. Для плоского напряжённого состояния условие (17 6) запишется так

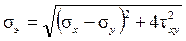£ R (17.7)

К недостатку теории можно отнести лишь то, что для объёмного напряжённого состояния не учитывается влияние на прочность промежуточного главного напряжения σ₂.

По сложившейся в сопротивлении материалов традиции критерий пластичности Треска – Сен-Венана обычно называют третьей теорией прочности.

IV. ЭНЕРГЕТИЧЕСКАЯ (ЧЕТВЁРТАЯ) ТЕОРИЯ ПРОЧНОСТИ

(Критерий пластичности Мизеса)

Данная теория основана на предположении, что напряжённые состояния равноопасны в том случае, если у них совпадает величина удельной потенциальной энергии формоизменения. Для общего случая объёмного напряжённого состояния удельная энергия изменения формы вычисляется по формуле (16.10):

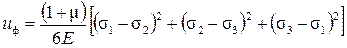
Для линейного напряжённого состояния, возникающего в растягиваемом стержне, получим

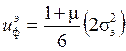
Приравняв эти выражения, выразим величину σ_э и сформулируем условие прочности по заданной теории:

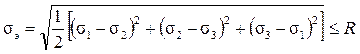(17.8)

В случае плоского напряжённого состояния, воспользовавшись (15.6), получим

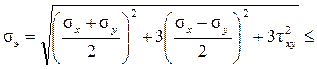R (17.9)

Энергетическая теория в принятой в настоящее время формулировке была предложена австрийским математиком и механиком Ричардом фон Мизесом (1883-1953 гг.). Как и третья теория прочности, она по сути устанавливает критерий появления в конструкции необратимых деформаций, причём результаты расчёта по этим теориям довольно близки и хорошо согласуются с экспериментами на образцах из пластичных материалов.

При некоторых частных видах нагружения расчёты по энергетической теории оказываются несколько точнее, чем по третьей теории.

V. ТЕОРИЯ ПРОЧНОСТИ МОРА

(пятая теория прочности)

В теории прочности, предложенной О.Мором, в отличии от остальных классических теорий не используется предположение о каком-то одном факторе, определяющем прочность. Напряжённое состояние в точке может быть графически представлено на плоскости σ - τ системой кругов Мора, построенных по главным напряжениям σ_1, σ_2, σ₃, как это показано на рис. 17.2.

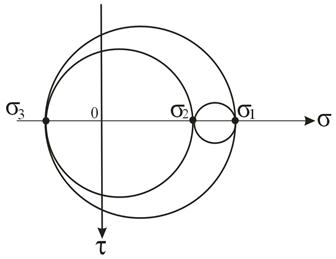
Рис. 17.2

Результаты опытов показывают, что наступление предельного состояния в основном определяется величиной наибольшего σ₁ и наименьшего σ₃ главных напряжений, и в гораздо меньшей степени зависит от напряжения σ₂. Поэтому при оценке прочности из трёх кругов можно использовать только наибольший, который называют главным кругом. Если при этом напряжения σ₁ и σ₃ таковы, что напряжённое состояние является предельным, соответствующий им главный круг также называют предельным кругом.

Получив на основе испытаний при различных соотношениях между главными напряжениями семейство предельных кругов, можно построить их огибающую, которая называется предельной огибающей. Она представляет собой кривую, пересекающую горизонтальную ось в точке C, соответствующей всестороннему растяжению. Многие материалы при сжатии выдерживают гораздо большие напряжения, чем при растяжении, поэтому диаметры показанных на рис. 17.3 предельных кругов увеличиваются по мере продвижения в область отрицательных нормальных напряжений. Слева предельная огибающая оказывается незамкнутой, поскольку при всестороннем сжатии материал способен выдержать не разрушаясь чрезвычайно большие нагрузки.

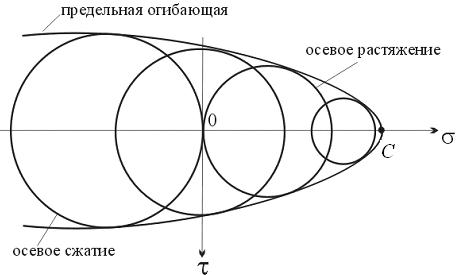
Рис. 17.3

Если главный круг, соответствующий напряжённому состоянию в опасной точке конструкции, лежит внутри предельной огибающей, то можно считать, что прочность обеспечена. При этом отношение диаметров предельного и найденного главного кругов представляет собой коэффициент запаса прочности. Проблема состоит лишь в том, что построение предельной огибающей для всей области возможных сочетаний напряжений на практике неосуществимо. Поэтому действительную огибающую схематизируют, заменяя прямыми, касательными к двум предельным кругам, соответствующим осевому растяжению и осевому сжатию, как это показано на рис. 17.4

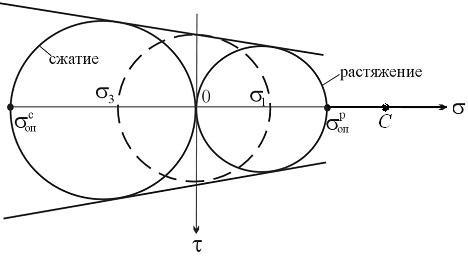
Рис. 17.4

Здесь 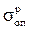, 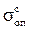- опасные напряжения при растяжении и сжатии.

При такой замене для любого напряженного состояния, главный круг которого касается этих прямых (на рис.17.4 он показан пунктиром), справедлива линейная зависимость

σ₁ = а + b σ₃ (17.10)

Коэффициенты а и b находятся из граничных условий:

1) при растяжении ,;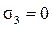

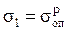2) при сжатии , .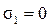

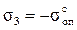Подставляя эти значения в (17.10), получаем

,

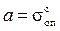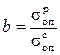. (17.11)

Выражение (17.10) приобретает вид

,

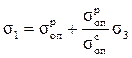или

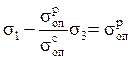
Отсюда следует условие прочности по данной теории

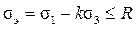(17.12)

Здесь R – расчётное сопротивление материала,

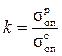- коэффициент, учитывающий различие прочностных свойств при растяжении и сжатии. Под опасными напряжениями σ_оп для пластичных материалов понимаются пределы текучести, для хрупких – пределы прочности. Для пластичных материалов величина k близка к единице, и теория прочности Мора даёт результат, совпадающий с третьей теорией. Отметим, что наиболее достоверный результат по теории Мора получается для напряжённых состояний, у которых главные напряжения σ₁ и σ₃ различны по знаку, т.е. главные круги лежат между предельными кругами для растяжения и сжатия.

Из рассмотренных теорий прочности в настоящее время широко используются лишь три: для пластичных материалов критерии Треска - Сен-Венана и Мизеса (третья и четвёртая теории), для хрупких – теория прочности Мора. Подчеркнём, что, говоря о пластичных и хрупких материалах, мы имеем в виду не только природу самого материала, но и условия нагружения – вид напряжённого состояния, температуру и скорость деформирования, существенно влияющие на его свойства.

Список рекомендуемой литературы

1. Александров А.В. Сопротивление материалов: учеб. для вузов / А.В. Александров, В.Д. Потапов, Б.П. Державин. – М.: Высш. шк., 2009. – 560 с.

2. Писаренко Г.С. Справочник по сопротивлению материалов / Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. – Киев: Дельта, 2008. – 813 с.

3. Феодосьев В.И. Сопротивление материалов: учеб. для вузов / В.И. Феодосьев. – М.: МГТУ им. Баумана, 2010. – 591 с.

4. Варданян Г.С. Сопротивление материалов (с основами строительной механики): учеб. для вузов / Г. С. Варданян, Н. М. Атаров, А. А. Горшков; Под ред. Г. С. Варданяна.— Москва: ИНФРА-М, 2003.— 478 с.

5. Саргсян А.Е. Сопротивление материалов, теории упругости и пластичности. Основы теории с примерами расчетов: учеб. для вузов / А. Е. Саргсян.— 2-е изд., испр. и доп.— Москва: Высш. шк, 2000.— 286 с.

6. Балакирев А.А. Справочные таблицы для выполнения учеб. заданий и курс. работ по курсу «Сопротивление материалов»/
А.А. Балакирев, В.Е. Калугин, Т.Э. Римм, Ю.П. Сметанников. – Пермь: Изд–во Перм. нац. исслед. политехн. ун-та, 2011. – 34 с.

Оглавление

Лекция 1. Введение.......................................................................................... 3

Лекция 2. Растяжение и сжатие..................................................................... 15

Лекция 3. Механические свойства конструкционных материалов.............. 26

Лекция 4. Геометрические характеристики плоских сечений...................... 41

Лекция 5. Сдвиг............................................................................................. 56

Лекция 6. Кручение....................................................................................... 64

Лекция 7. Изгиб прямого стержня................................................................ 75

Лекция 8. Напряжение в балке при чистом изгибе...................................... 90

Лекция 9. Напряжения в балке при поперечном изгибе.............................. 96

Лекция 10. Определение перемещений при изгибе.................................... 109

Лекция 11. Общие методы определения перемещений

в упругих системах...................................................................................... 121

Лекция 12. Статически неопределимые стержневые системы................... 137

Лекция 13. Учет свойств симметрии при раскрытии статической неопределимости методом сил................................................................................................. 147

Лекция 14. Основы теории напряженного и деформированного

состояния..................................................................................................... 151

Лекция 15. Плоское напряженное состояние............................................. 158

Лекция 16. Элементы теории деформированного состояния

в точке тела.................................................................................................. 170

Лекция 17. Теории прочности.................................................................... 179

Список рекомендуемой литературы........................................................... 187

Дата добавления: 2014-01-06