Тема 2. Математические модели игр

Рассмотрим парную игру с игроками А и В. Пусть игрок А имеет т стратегий - , а (противник) игрок В - п стратегий 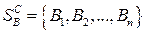. Натуральные числа т и п в общем случае никак не связаны между собой.

Если каждый из игроков А и В сознательно определенным образом выбирает стратегии и соответственно, то сложившаяся ситуация (в чистых стратегиях) однозначно определяет выигрыш игрока А, выражающийся действительным числом , которое одновременно является и проигрышем игрока В. А число 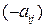выражает проигрыш игрока А и выигрыш игрока В. Если число отрицательно, то в принятой нами формализованной терминологии оно будет представлять отрицательный выигрыш игрока А, а по сути - его проигрыш. Числа - это значения функции выигрыша 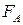игрока А: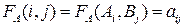. Ходы игроков с сознательным выбором одной из возможных своих чистых стратегий называют иногда личными ходами.

Выигрыши , , можно расположить в виде матрицы, номера строк которой соответствуют номерам стратегий игрока А, а номера столбцов - номерам стратегий игрока В.

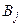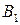
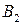
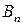
А =	Ai			…		(4.1)
			…
			…
…	…	…	…	…
			...

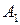
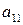
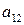
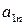
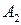
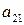
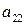
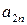
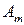
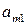
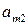
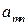
Матрица А называется матрицей выигрышей игрока А. Обозначим через значения функции выигрыша Р_в игрока В, т. е. ед, 0 = Рв (В;, Ад = =1,..., п, 1 =1,..., т. Тогда матрица выигрышей игрока В будет иметь вид

B =	Ai			…
			…
			…
…	…	…	…	…
			...

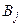
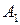
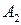
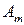
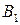
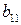
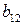
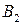
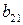
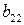
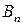
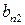
Если рассматриваемая игра – антагонистическая (т.е. с нулевой сумой выигрышей), то функции выигрышей 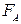и игроков A и B связаны между собой равенством (3.1) и, следовательно,

Эти равенства означают, что матрица выигрышей B игрока B является противоположной транспонированной матрице A:

.

Таким образом, матрица В вполне определяется матрицей А. Матрицу А также называю матрицей игры, или платежной матрицей. Матрица А имеет размер , где первая компонента размера 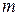указывает на число строк (т.е. число стратегий игрока А), а вторая 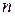- на число столбцов (число стратегий игрока В). Поэтому часто такую игру называют - игрой.

Отметим, что матрица игры существенно зависит от упорядочения множеств 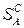и стратегий игроков А и В. При другой нумерации стратегий этих множеств мы получим, вообще говоря, другую матрицу игры. Так что одна и та же игра может описываться различными матрицами. Но при всех возможных матрицах игры функция 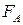выигрыша игрока А остается одной и той же, определенной на декартовом произведении 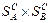с множеством значений в множестве действительных чисел R. Это замечание относится и к функции 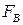выигрыша игрока В.

Построение матрицы выигрышей может представлять весьма нетривиальную задачу, особенно для игр большой размерности. В принципе же всякую конечную антагонистическую игру можно привести к матричной форме.

Матрица игры А формируется в зависимости от значений функции выигрыша 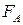, которая может задаваться таблично, аналитически (в виде формулы) или словестно-описательным способом.

Для того чтобы совокупность 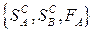, представляющая антагонистическую игру, стала обозримой, необходимо перечислить возможные стратегии игроков, т.е. сформировать множества 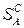и , и формализовать правила, по которым развивается конфликт, в виде функции выигрыша .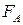

Пример 4.1 (антагонистическая конкуренция) [7]. Фирма А производит некоторый сезонный товар, имеющий спрос в течение 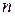единицвремени, и который она может поставить на рынок в один из моментов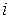 (см. рис. 4.1).

Для конкурентной борьбы с фирмой А дочерняя фирма В концерна D не заботясь о собственных доходах, производит аналогичный товар, который поступает на рынок в один из моментов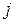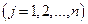. Цель фирмы В - разорение фирмы А, после чего, используя капитал концерна D она может легко наверстать упущенное. Единственным законным средством фирмы В в конкурентной борьбе является выбор момента поставки товара на рынок, так как понижение цены на поставляемый товар запрещено определенным соглашением. Для разорения фирмы А фирма В должна минимизировать ее дохода. Пусть технология выпуска товара такова, что чем дольше он находится в производстве, и, следовательно, позже поступает на рынок, тем выше его качество, а реализуется товар только более высокого качества (так как цена на товары разного качества одна и та же). Доход от продажи товара в единицу времени составляет с денежных единиц.

Требуется построить функцию выигрыша фирмы А, где под выигрышем понимается в данном случае доход этой фирмы, зависящий от складывающихся ситуаций. Используя функцию выигрыша, надо составить матрицу игры для случая и выписать конкретный вид этой матрицы, который она приобретает в случае, когда доход денежным единицам.

Пример 4.2. На каждой из двух торговых баз ассортиментный минимум составляет один и тот же набор из 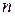видов товаров. Каждая база должна поставить в свой магазин только один из этих видов товара. Магазины, обозначим их А и В, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако, товар, поставляемый в магазин В, более высокого качества. Если магазин А завезет с базы товар 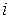-го вида , отличный от товара 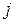-го вида 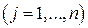, завезенного в магазин В, то товар го вида будет пользоваться спросом и магазин А от его реализации получит прибыль денежных единиц. 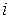Если же в магазины А и В завезены товары одинакового вида, то товар -го вида в магазине А спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества, можно купить в магазине В, и потому магазин А понесет убытки по транспортировке, хранению и возможно порче товара 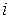-го вида в размере денежных единиц.

Требуется формализовать данную конфликтную ситуацию и построить матрицу игры при .

Дата добавления: 2014-01-06