Тема 5. Смешанные стратегии

Среди антагонистических игр, моделирующих практические конфликты, существенную долю составляют игры без седловых точек, т.е. игры, в которых нижняя цена игры 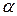строго меньше верхней цены 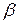: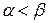. Если такая игра состоит из единственной "партии", т.е. каждый из игроков А и В делает только один ход, предполагая, что его соперник играет разумно, то осторожность поведения мотивирует выбор игроком А одной из своих максиминных стратегий, а игроком В - одной из своих минимаксных стратегий. В этом случае игрок А обеспечивает себе выигрыш, не меньший нижней цены игры 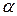, а игрок В гарантирует, что выигрыш игрока А будет не больше верхней цены игры .

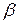Стратегия игрока» состоящая в случайном выборе одной из его чистых стратегий, называется смешанной стратегией. Таким образом, смешанная стратегия игрока представляет собой дискретную случайную величину, значениями которой являются номера его чистых стратегий.

При условии, что множество 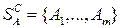чистых стратегий игрока А известно, каждая его смешанная стратегия Р определяется вероятностями 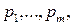с которыми выбираются игроком А соответствующие чистые стратегии. Поэтому смешанную стратегию Р можно отождествить с 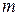-мерным вектором 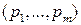, т.е.

.

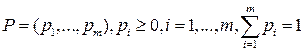То же относится и к смешанным стратегиям игрока B:

.

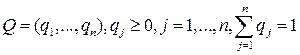Обозначим через

.

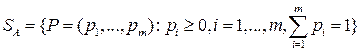Каждую чистую стратегию 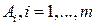, игрока А можно рассматривать как смешанную стратегию

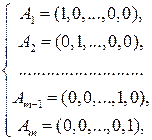(5.1)

Таким образом, каждую смешанную стратегию можно представить линейной комбинацией чистых стратегий с коэффициентами, являющимися координатами данной смешанной стратегии:

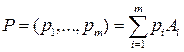. (5.2)

Представления (5.1) и (5.2) дают возможность геометрически проинтерпретировать конфигурацию множеств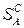 и 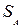чистых и смешанных стратегий соответственно.

Руководствуясь приведенными определениями, мы видим, что правая часть равенства (у.2) является выпуклой комбинацией орт 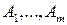(см. (5.1)) и потому множество 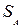всех смешанных стратегий геометрически представляет собой фундаментальный 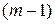-мерный симплекс с 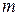вершинами в точках 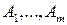, представляющих чистые стратегии (выпуклая оболочка, натянутая на чистые стратегии).

Дата добавления: 2014-01-06