Тема 6. Функции выигрыша в смешанных стратегиях

Примеры симплексов

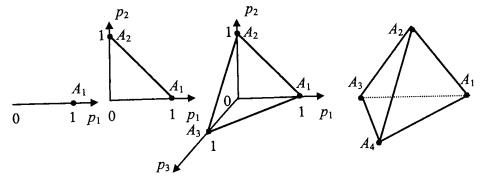
Если игроки А и В независимо друг от друга выбрали смешанные стратегии соответственно 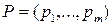и 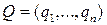, то упорядоченная пара (Р, Q) называется ситуацией в смешанных стратегиях. В условиях ситуации (Р, Q) в смешанных стратегиях чистые стратеги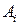и и 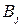выбираются независимо друг от друга случайным образом с вероятностями соответственно 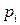и 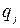. Поэтому вероятность совместного выбора чистых стратегий 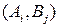равна произведению их вероятностей: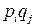. Но в ситуации 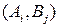в чистых стратегиях игрок А получает выигрыш . Вероятность этого выигрыша совпадает с вероятностью ситуации 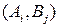, т. е. равна .

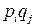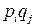Таким образом, выигрыш игрока А в ситуации (Р, Q) в смешанных стратегиях представляет собой дискретную случайную величину, принимающую значения с вероятностью . Тогда средний выигрыш игрока А в ситуации (Р, Q) в смешанных стратегиях есть математическое ожидание указанной случайной величины

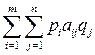(6.1)

Определим функцию выигрыша игрока А в смешанных стратегиях как функцию H, заданную на декартовом произведении 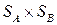множеств смешанных стратегий, ставящую в соответствие каждой ситуации 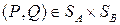в смешанных стратегиях средний выигрыш игрока А в этой ситуации, определяемый выражением (8.1). Таким образом,

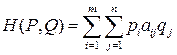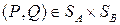, , (6.2)

где , .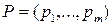

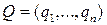Форма (6.2) задания функции выигрыша в смешанных стратегиях называется координатной. Функцию Н можно задать и в матричной форме

,

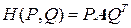Теорема 6.1. Для каждой смешанной (в частности, чистой) стратегии игрока А существует (достигается)

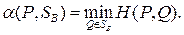(6.2)

Для каждой смешанной (в частности, чистой) стратегии е8_в игрока В существует (достигается)

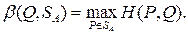(6.3)

Число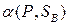, определенное равенством (6.2) (существование которого доказано в теореме 6.1), назовем показателем эффективности смешанной стратегии 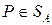игрока А относительно множества 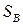смешанных стратегий игрока В.

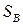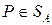Если в этом определении множество смешанных стратегий игрока В заменить на множество его чистых стратегий, то получим определение показателя эффективности смешанной стратегии игрока А относительно множества чистых стратегий игрока В:

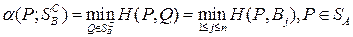. (6.4)

Теорема 6.2. Показатели эффективности любой смешанной (в частности, чистой) стратегии 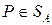игрока А относительно множеств и 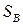чистых и смешанных стратегий противника В равны, т.е.

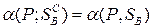(6.5)

Число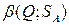, определенное равенством (6.3), назовем показателем неэффективности смешанной стратегии 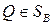игрока В относительно множества 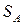смешанных стратегий игрока А, а число

(6.6)

показателем неэффективности смешанной стратегии Q игрока В относительно множества 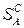чистых стратегий игрока А.

Теорема 6.3. Показатели неэффективности любой смешанной (в частности, чистой) стратегии 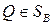игрока В относительно множеств 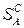и 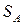чистых и смешанных стратегий игрока А равны, т.е.

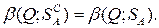
Нижней ценой (или максимином) матричной игры в смешанных стратегиях называется величина

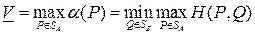
Верхней ценой (или минимаксом) матричной игры в смешанных стратегиях называется величина

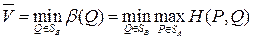
Те о р е м а 6.4. Для любой конечной матричной игры существуют нижняя и верхняя цены игры в смешанных стратегиях.

Соотношения между нижними и верхними ценами игры в чистых и смешанных стратегиях устанавливаются в следующей теореме.

Теорема 6.5. Нижняя цена игры а и верхняя цена игры (3 в чистых стратегиях, нижняя цена игры V и верхняя цена игры

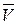в смешанных стратегиях удовлетворяют следующему неравенству

.

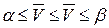Дата добавления: 2014-01-06