Тема 9. Принцип доминирования

Отыскать решения игр без седловой точки, особенно при достаточно больших размерах платежной матрицы, оказывается довольно сложной задачей. В некоторых случаях эту задачу можно упростить с помощью редуцирования игр, т. е. сведения данной игры со сложной матрицей к игре с более простой матрицей. В этом параграфе мы рассмотрим один из способов редуцирования игр, основанный на принципе доминирования, который позволяет в некоторых случаях игру с матрицей большего размера свести к игре с матрицей меньшего размера.

Пусть имеем игру с матрицей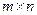

А =	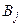Ai			…
			…
			…
…	…	…	…	…
			...

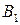
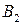
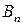
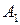
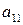
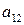
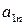
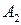
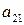
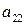
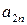
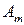
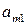
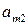
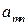
Каждой смешанной (в частности, чистой) стратегии 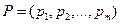игрока А поставим в соответствие строку

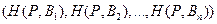(9.1)

Строку (9.1) можно представить так:

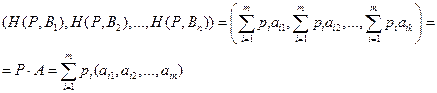(9.2)

Обратно, каждой выпуклой комбинации (9.2) строк матрицы А с коэффициентами поставим в соответствие смешанную стратегию 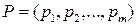игрока А.

Таким образом, между смешанными (в том числе и чистыми) стратегиями 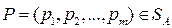игрока А и выпуклыми комбинациями

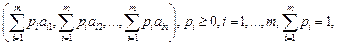
строк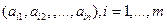матрицы А устанавливается взаимно-однозначное соответствие

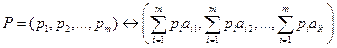(9.3)

Из (9.1) или (9.3) ясно, что каждой чистой стратегии 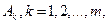игрока А ставится во взаимно-однозначное соответствие k-я строка 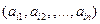матрицы А.

Если для двух выпуклых комбинаций строк матрицы А

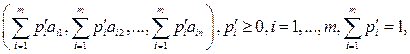(9.4)

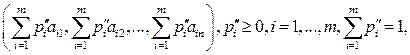(9.5)

выполняются неравенства

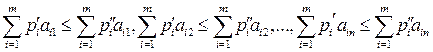, (9.6)

то говорят, что строка (9.5) доминирует строку (9.4), а строка (9.4) доминируется строкой (9.5). Таким образом, строка (11.5) — доминирующая строку (9.4), а строка (9.4) — доминируемая строкой (9.5).

Если каждое из неравенств (9.6) является равенством, то строки (9.4) и (9.5) называют дублирующими друг друга. Каждая из двух дублирующих строк является одновременно и доминируемой, и доминирующей другую.

Если каждое из неравенств (9.6) является строгим, то говорят, что строка (9.5) строго доминирует строку (9.4), а строка (9.4) строго доминируется строкой (9.5), или строка (9.5) является строго доминирующей строку (9.4), а строка (9.4) является строго доминируемой строкой (9.5).

Аналогичная терминология используется и для соответствующих стратегий игрока А. А именно, если строка (9.5) доминирует, соответственно дублирует, соответственно строго доминирует строку (9.4), то говорят, что стратегия 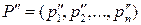доминирует, соответственно дублирует, соответственно строго доминирует стратегию .

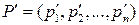Так как элементами строк, соответствующих по (9.3) смешанным стратегиям, являются выигрыши игрока А (см. (9.1)), то из данных определений понятно, что для игрока А дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо для него невыгодна.

Аналогично, каждой смешанной (в частности, чистой) стратегии 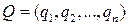игрока В поставим в соответствие столбец

(9.7)

Если для двух выпуклых комбинаций столбцов матрицы А

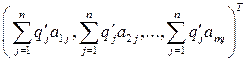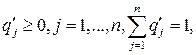, (9.8)

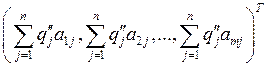
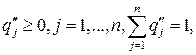(9.9)

справедливы неравенства

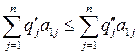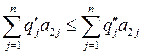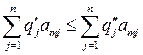, ,...,, (9.10)

то говорят, что столбец (9.8) (стратегия 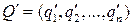) доминирует столбец (9.9) (стратегию 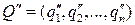) а столбец (9.9) (стратегия ) доминируется столбцом (9.8) (стратегией ).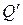

В случае, когда каждое неравенство (9.10) является равенством, столбцы (9.8) и (9.9) (стратеги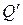и и ) называются дублирующими.

Если каждое неравенство (9.10) является строгим, то столбец (9.8) (стратегия 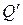) называется строго доминирующим (строго доминирующей) столбец (9.9) (стратегию ), а столбец (11.11) (стратегия ) - строго доминируемым (строго доминируемой) столбцом (11.10) (стратегией ).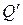

Теорема 9.1. Справедливы следующие предложения.

1 .Если 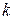-я строка, , матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее строк, то существует оптимальная смешанная стратегия 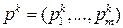игрока А, в которой 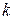-я чистая стратегия 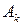выбирается им с нулевой вероятностью, т.е.

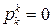2. Если 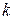-я строка, , матрицы 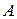игры строго доминируется некоторой выпуклой комбинацией остальных ее строк, то в любой оптимальной смешанной стратегии 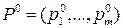игрока А чистая 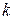-я стратегия 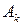выбирается им с нулевой вероятностью, т.е..

3. Если 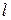-й столбец,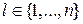, матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее столбцов, то существует оптимальная смешанная стратегия 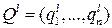игрока В, в которой 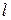-я чистая стратегия 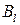выбирается им с нулевой вероятностью, т.е. .

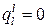4. Если 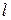-й столбец, 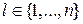, матрицы А игры строго доминируется некоторой выпуклой комбинацией остальных ее столбцов, то в любой оптимальной смешанной стратегии 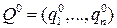игрока В чистая 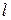-я стратегия 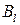выбирается им с нулевой вероятностью, т е..

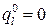Следствие 9.1.

1. Если 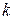-я строка матрицы игры доминируется (строго доминируется) некоторой другой строкой, то существует (любая) оптимальная смешанная стратегия игрока А, в которую чистая стратегия 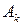входит с нулевой вероятностью.

2. Если 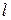-й столбец матрицы игры доминируется (строго доминируется) некоторым другим столбцом, то существует (любая) оптимальная смешанная стратегия игрока В, в которую чистая стратегия 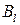входит с нулевой вероятностью.

Следствие 9.2 (о дублирующих чистых стратегиях). Одну из двух дублирующих чистых стратегий можно удалить.

Пример 11.1. Рассмотрим игру 3x5 с матрицей

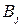
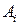
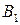
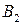
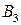
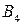
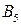
						(9.11)
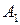
	-2
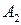
	-1	-4		-1	-4
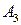
		-5			-5

В данной матрице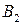и 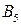- дублирующие стратегии игрока В. Поэтому в соответствии со следствием 9.2 один из этих столбцов можно удалить. Удалим, например, 5-й столбец. В оставшейся матрице 3-й Столбец строго, а 4-й столбец нестрого доминируются 1-м столбцом. Поэтому можно удалить также 3-й и 4-й столбцы. В результате получим матрицу

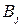
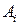
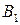
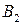
			(9.12)
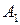
	-2
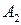
	-1	-4
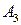
		-5

2-я строка матрицы (9.12) строго доминируется выпуклой комбинацией 1-й и 3-й строк с коэффициентам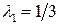ии :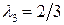

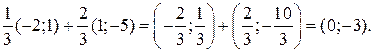
Поэтому нужно отбросить 2-ю строку. В результате получим матрицу

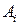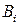
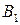
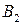
			(9.13)
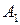
	-2
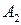
		-5

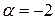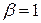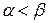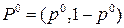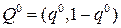Нижняя цена в чистых стратегиях игры с матрицей (11.25) , а верхняя цена . Так как , то решение надо искать в смешанных стратегиях. Предположим, что и - оптимальные стратегии игроков и V - цена игры с матрицей (9.13). Тогда по необходимым условиям оптимальности стратегий, сформулированным в теореме 9.2, имеем:

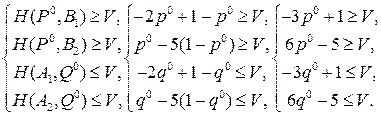(9.14)

Умножив 1-е неравенство системы (9.14) на 2 и прибавив ко 2-му, получим

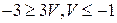(9.15)

Умножив 3-е неравенство системы (9.4) на 2 и прибавив к 4-му, получим

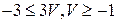(9.16)

Из неравенств (9.15) и (9.16) следует равенство 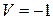. Подставим найденное значение V в систему (9.15):

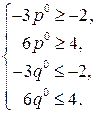(11.29)

Из первых двух уравнений системы (11.29): , а из вторых двух уравнений:.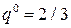

Учитывая удаленные столбцы и строку для исходной игры с матрицей (11.11), получим следующее (частное) решение:

.

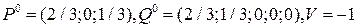Поскольку 4-й столбец матрицы (11.23) нестрого доминировался 1-м столбцом, то могут существовать и другие оптимальные стратегии игрока В, в которых чистая стратегия 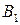будет входить с положительной вероятностью.

Дата добавления: 2014-01-06