Тема 10. Игры 2хп

Рассмотрим игру с матрицей

				…
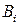
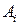
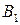
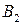
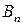
A=				…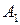
				…

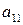
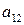
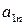
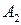
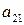
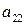
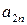
В этой игре игрок А обладает двумя чистыми стратегиям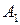и и 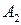, а игрок В имеет п чистых стратегий , ,…,.

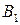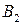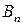Известно, что показатель эффективности стратегии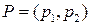

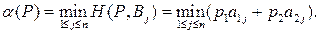
Если 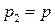, то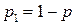, поскольку 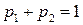. Тогда 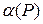будет выражаться формулой

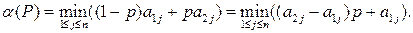
Таким образом, 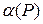представляет собой нижнюю огибающую п линейных функций 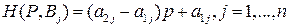, от вероятности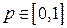, график каждой из которых есть отрезок, возрастающий (положительного наклона), убывающий (отрицательного наклона) или горизонтальный, в зависимости от того, положителен, отрицателен или равен нулю угловой коэффициент 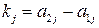этой линейной функции.

Стратегия 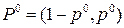, удовлетворяющая равенству

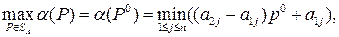(10.1)

где, напомним, 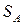- множество всех смешанных (в том числе и чистых) стратегий игрока А, является (по основной теореме 8.1 матричных игр фон Неймана, см. [9])) оптимальной, т.е. абсцисса 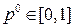максимальной (наивысшей) точки нижней огибающей 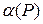определяет оптимальную стратегию 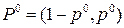, придерживаясь которой игрок А выбирает свои чистые стратегии случайным образом, причем стратегию - с вероятностью 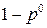, а стратегию 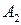- с вероятностью .

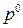По теореме фон Неймана

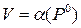, (10.2)

т.е. цена игры V равна ординате максимальной точки нижней огибающей.

Таким образом, мы можем сформулировать алгоритм геометрического (графического) нахождения оптимальных стратегий игрока А и цены игры.

Алгоритм "А "

1. Берем горизонтальный отрезок [0,1].

2. Через концы отрезка [0,1] проводим к нему два перпендикуляра: левый и правый.

3. На левом перпендикуляре, лежащем на вертикальной числовой оси, от точки 0 его пересечения с отрезком [0,1] откладываем все элементы первой строки матрицы А.

4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второй строки матрицы А.

Замечания к пунктам 1, 3, 4. Масштабы на левом и правом перпендикулярах должны быть одинаковыми, не обязательно совпадающими с масштабом горизонтального отрезка [0,1].

5. Каждую пару точек, изображающих элементы 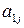и 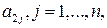стоящие в 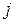-м столбце матрицы А, соединяем отрезком 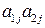. Таким образом, будут построены 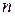отрезков, представляющих собой графики 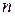линейных функций

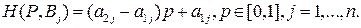(10.3)

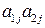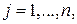
6. Если все отрезки ,- неубывающие (имеют неотрицательный наклон): 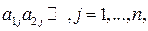, то стратегия 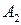доминирует стратегию 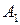. Если все отрезки 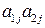,,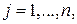 возрастающие (имеют положительный наклон): 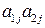, 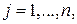то стратегия 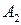строго доминирует стратегию .

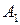7. Если все отрезки 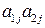,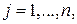невозрастающие (имеют неположительный наклон): 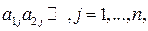то стратегия 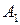доминирует стратегию 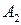. Если все отрезки 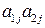,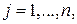убывающие (имеют отрицательный наклон): 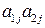, 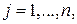то стратегия 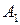строго доминирует стратегию .

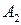8. Если отрезок 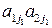лежит не ниже отрезка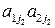, ,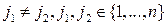то стратегия 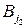доминирует стратегию . Если отрезок 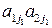лежит выше отрезка 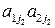, , 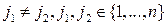то стратегия 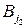строго доминирует стратегию .

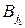9. Находим (выделяем) нижнюю огибающую (10.1) семейства отрезков (10.3), которая в общем случае будет представлять собой выпуклую вверх ломаную, а, в частности, может быть и отрезком.

10. На нижней огибающей находим максимальную (наивысшую) точку (или точки).

11. Абсцисса 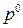этой точки (удовлетворяющая равенству (10.1)) является вероятностью выбора игроком А чистой стратегии А₂ в оптимальной смешанной стратегии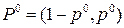

12. Ордината наивысшей точки нижней огибающей является ценой игры V (см. 10.2)).

13. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях .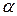

14. Нижний из верхних концов отрезков 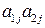,,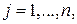 есть верхняя цена игры в чистых стратегиях .

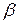15. Элемент матрицы А, изображающая точка которого является нижней на перпендикуляре, где она лежит, и верхним концом отрезка, на котором она лежит, будет седловой точкой игры.

В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.

Рис. 10.1

На рис. 10.1 из 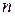отрезков 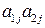,,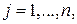 указаны три, которые принимают участие в конструировании нижней огибающей, выделенной жирной линией; N - максимальная точка этой огибающей; р° - абсцисса точки N, следовательно 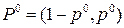- оптимальная смешанная стратегия игрока А: цена игры V равна ординате точки N; нижняя цена игры в чистых стратегиях 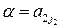; верхняя цена игры в чистых стратегиях 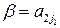; на рисунке видно, что .

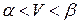Теорема 16.1. Если через максимальную точку N нижней огибающей отрезков 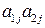, 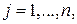порождаемых чистыми стратегиями 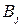, 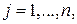игрока В, проходят два каких-либо отрезка 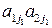,,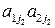 , 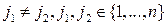то абсцисса

точки N

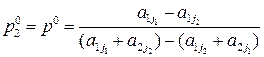(10.4)

и, следовательно,

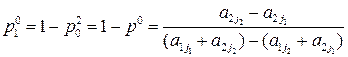, (10.5)

а цепа игры

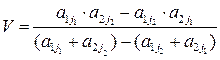. (16.7)

Теорема 16.2. Пусть через максимальную точку N нижней огибающей отрезков 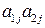, 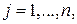порождаемых чистыми стратегиями 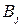, 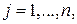игрока В, проходят два каких-либо отрезка ,, .

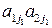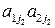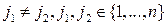Для того чтобы смешанная стратегия 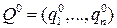игрока В, где

,

,

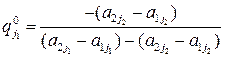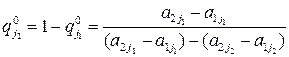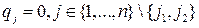
была оптимальной, необходимо и достаточно, чтобы отрезк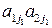и и 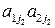имели разные наклоны.

Тема 11. Игры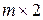

В этом параграфе рассмотрим игру 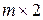, в которой игрок 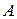обладает 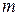чистыми стратегиями 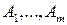, а игрок 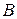- двумя чистыми стратегиям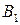и и 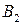. Матрица игры имеет вид

A=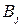
…	…	…

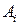
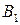
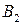
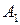
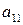
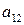
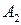
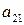
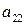
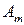
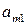
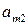
Известно, что показатель неэффективности 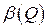стратегии 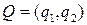, , 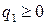, , 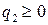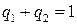игрока 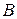имеет вид

.

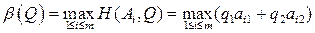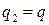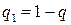Если обозначить , то и

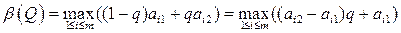. (11.1)

Таким образом, показатель неэффективности 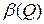стратегии 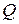есть верхняя огибающая 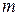линейных функций 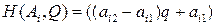, 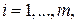зависящих от вероятности 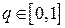, график каждой из которых представляет собой отрезок определенного наклона в зависимости от знака углового коэффициента 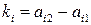этой функции.

Если стратегия 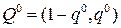удовлетворяет равенству

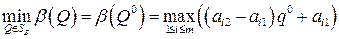(11.2)

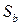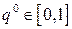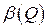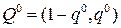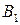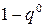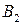где — множество всех смешанных стратегий игрока В, то по основной теореме фон Неймана она является оптимальной. Таким образом, абсцисса минимальной (наинизшей) точки верхней огибающей определяет оптимальную стратегию ,по которой игрок В случайным образом выбирает свои чистые стратегии с вероятностью и с вероятностью .

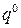По той же теореме фон Неймана цена игры

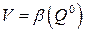, (11.3)

т. е. цена игры V равна ординате минимальной точки верхней огибающей.

Из сказанного легко сформулировать алгоритм "В" геометрического нахождения оптимальных стратегий игрока В и цены игры V (см. рис. 17.1).

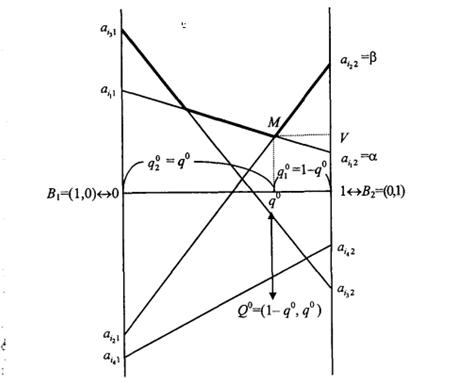
Рис. 11.1

Алгоритм "В"

1. Берем горизонтальный отрезок [0,1].

2. Через концы отрезка [0,1] проводим к нему два перпендикуляра: левый и правый.

3. На левом перпендикуляре, лежащем на вертикальной числовой оси, от точки 0 его пересечения с отрезком [0,1] откладываем все элементы первого столбца матрицы А.

4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второго столбца матрицы А.

5. Каждую пару точек, изображающих элементы 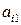и 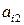, 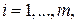стоящие в 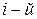строке матрицы А, соединяем отрезком 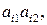в результате чего построим 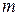отрезков, представляющих собой графики 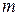линейных функций

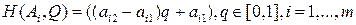(11.4)

6. Если все отрезки 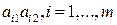, имеют неотрицательный наклон, т. е. положительный или нулевой (другими словами, все отрезки 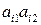- неубывающие: 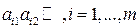, то стратегия 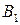, доминирует стратегию 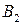. Если все отрезки 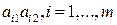, имеют положительный наклон, т. е. являются возрастающими: 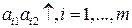, то стратегия 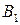строго доминирует стратегию .

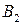7. Если все отрезки 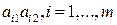, имеют неположительный наклон, т. е. отрицательный или нулевой (другими словами, все отрезки 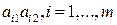, - невозрастающие: 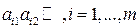, то стратегия 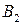доминирует стратегию 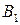. Если все отрезки 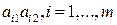, имеют отрицательный наклон, т. е. являются убывающими: 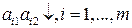, то стратегия 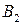строго доминирует стратегию .

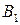8. Отрезок 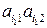лежит не ниже отрезка 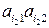,,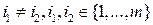 то стратегия 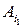доминирует стратегию 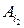. Если отрезок 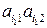лежит выше отрезка 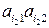,,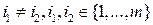 то стратегия 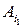строго доминирует стратегию .

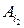9. Находим (выделяем) верхнюю огибающую (17.1) семейства отрезков (17.4), представляющую собой в общем случае выпуклую вниз ломаную, которая, в частности, может быть и отрезком.

10. На верхней огибающей находим минимальную (наинизшую) точку (точки).

11. Абсцисса 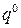минимальной точки (удовлетворяющая равенству (17.2)) является вероятностью случайного выбора игроком В чистой стратегии В2 в оптимальной смешанной стратегии .

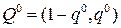12. Ордината минимальной точки верхней огибающей является ценой игры 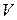(см. (17.3)).

13. Верхний из нижних концов отрезков 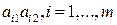, является нижней ценой игры в чистых стратегиях .

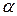14. Нижний из концов верхней огибающей (лежащих на перпендикулярах) является верхней ценой игры в чистых стратегиях .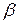

15. Элемент матрицы А, представленный на рисунке точкой являющейся нижним концом отрезка, на котором она лежит, и верхним на перпендикуляре, которому она принадлежит, является седловой точкой игры. В этом случае чистая стратегия игрока А, номер которой совпадает с первым индексом седловой точки, является оптимальной.

На рис. 17.1 из т отрезков 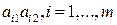, указаны четыре 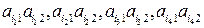, первые три из которых принимают участие в конструировании верхней огибающей, выделенной" жирной линией. Точка М - минимальная точка этой верхней огибающей, имеющая своей абсциссой 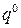. Поэтому 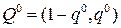- оптимальная смешанная стратегия игрока В. Ордината точки М есть цена игры V. Нижняя цена игры в чистых стратегиях 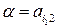, верхняя цена игры в чистых стратегиях 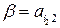. Так как среди отрезков 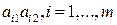- имеются отрезки с положительным и отрицательным наклонами (например, отрезок 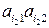имеет положительный наклон, а отрезок 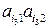- отрицательный), то стратегия В₂ не доминирует и не доминируется стратегией 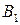. 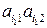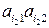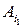Так как отрезки и лежат выше отрезка , то каждая из стратегий и 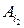строго доминирует стратегию . Оптимальную стратегию 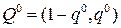игрока В и цену игры V можно подсчитать и по формулам, которые даются в следующей теореме.

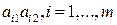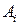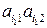Теорема 11.1. Если через минимальную точку М верхней огибающей отрезков , порождаемых чистыми стратегиями , , игрока А, проходят два каких-либо отрезка и 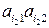,,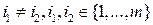 то абсцисса точки М

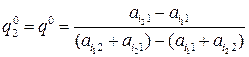
и, следовательно,

,

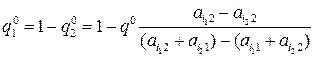а цена игры

.

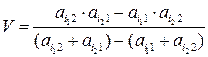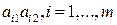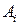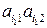Теорема 11.2. Пусть через минимальную точку М верхней огибающей отрезков , порождаемых чистыми стратегиями А, , игрока А, проходят два каких-либо отрезка и ,.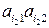

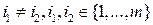Для того чтобы смешанная стратегия 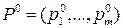игрока А, где

,

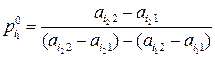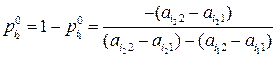
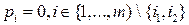
была оптимальной, необходимо и достаточно, чтобы отрезк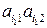и и 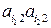, имели разные наклоны.

Дата добавления: 2014-01-06